{sdmgamindex} case study with and without covariates
March 11 2024
D-simple-case-study.RmdCheck your system:
sessionInfo()
#> R version 4.3.1 (2023-06-16 ucrt)
#> Platform: x86_64-w64-mingw32/x64 (64-bit)
#> Running under: Windows 10 x64 (build 19045)
#>
#> Matrix products: default
#>
#>
#> locale:
#> [1] LC_COLLATE=English_United States.utf8
#> [2] LC_CTYPE=English_United States.utf8
#> [3] LC_MONETARY=English_United States.utf8
#> [4] LC_NUMERIC=C
#> [5] LC_TIME=English_United States.utf8
#>
#> time zone: America/Los_Angeles
#> tzcode source: internal
#>
#> attached base packages:
#> [1] parallel stats graphics grDevices utils datasets methods
#> [8] base
#>
#> other attached packages:
#> [1] coldpool_3.3-1 viridis_0.6.5 stringr_1.5.1 reshape2_1.4.4
#> [5] lubridate_1.9.3 fields_15.2 viridisLite_0.4.2 spam_2.10-0
#> [9] ggthemes_5.1.0 akgfmaps_3.4.2 terra_1.7-71 stars_0.6-4
#> [13] abind_1.4-5 ggplot2_3.5.0 classInt_0.4-10 raster_3.6-26
#> [17] flextable_0.9.4 magrittr_2.0.3 gstat_2.1-1 dplyr_1.1.4
#> [21] DATRAS_1.01 sdmgamindex_0.1.1 tweedie_2.3.5 MASS_7.3-60.0.1
#> [25] sf_1.0-15 sp_2.1-3 RANN_2.6.1 marmap_1.0.10
#> [29] mapdata_2.3.1 maps_3.4.2 tidyr_1.3.1 mgcv_1.9-1
#> [33] nlme_3.1-164
#>
#> loaded via a namespace (and not attached):
#> [1] rstudioapi_0.15.0 jsonlite_1.8.8 shape_1.4.6.1
#> [4] rmarkdown_2.25 fs_1.6.3 ragg_1.2.7
#> [7] vctrs_0.6.5 memoise_2.0.1 askpass_1.2.0
#> [10] htmltools_0.5.7 curl_5.2.1 sass_0.4.8
#> [13] KernSmooth_2.23-22 bslib_0.6.1 desc_1.4.3
#> [16] plyr_1.8.9 zoo_1.8-12 cachem_1.0.8
#> [19] uuid_1.2-0 igraph_2.0.2 mime_0.12
#> [22] lifecycle_1.0.4 pkgconfig_2.0.3 Matrix_1.6-5
#> [25] R6_2.5.1 fastmap_1.1.1 shiny_1.8.0
#> [28] digest_0.6.34 colorspace_2.1-0 rprojroot_2.0.4
#> [31] textshaping_0.3.7 RSQLite_2.3.5 fansi_1.0.6
#> [34] timechange_0.3.0 gdistance_1.6.4 compiler_4.3.1
#> [37] here_1.0.1 proxy_0.4-27 intervals_0.15.4
#> [40] bit64_4.0.5 fontquiver_0.2.1 withr_3.0.0
#> [43] DBI_1.2.2 openssl_2.1.1 icesDatras_1.4.1
#> [46] gfonts_0.2.0 tools_4.3.1 units_0.8-5
#> [49] zip_2.3.1 httpuv_1.6.14 glue_1.7.0
#> [52] promises_1.2.1 grid_4.3.1 generics_0.1.3
#> [55] gtable_0.3.4 class_7.3-22 data.table_1.15.2
#> [58] xml2_1.3.6 utf8_1.2.4 pillar_1.9.0
#> [61] later_1.3.2 splines_4.3.1 lattice_0.22-5
#> [64] FNN_1.1.4 bit_4.0.5 tidyselect_1.2.0
#> [67] fontLiberation_0.1.0 knitr_1.45 gridExtra_2.3
#> [70] fontBitstreamVera_0.1.1 crul_1.4.0 xfun_0.42
#> [73] adehabitatMA_0.3.16 stringi_1.8.3 yaml_2.3.8
#> [76] evaluate_0.23 codetools_0.2-19 httpcode_0.3.0
#> [79] officer_0.6.5 gdtools_0.3.7 tibble_3.2.1
#> [82] cli_3.6.2 xtable_1.8-4 systemfonts_1.0.5
#> [85] munsell_0.5.0 jquerylib_0.1.4 spacetime_1.3-1
#> [88] Rcpp_1.0.12 ellipsis_0.3.2 pkgdown_2.0.7
#> [91] blob_1.2.4 dotCall64_1.1-1 scales_1.3.0
#> [94] xts_0.13.2 e1071_1.7-14 ncdf4_1.22
#> [97] purrr_1.0.2 crayon_1.5.2 rlang_1.1.3Case study
In this example, we will use data from NOAA Fisheries’ eastern Bering sea (EBS) bottom trawl survey. The Resource Assessment and Conservation Engineering (RACE) Division Groundfish Assessment Program (GAP) of the Alaska Fisheries Science Center (AFSC) conducts fisheries-independent bottom trawl surveys to assess the populations of demersal fish and crab stocks of Alaska. The species covered in this case study include yellow fin sole, walleye pollock, and red king crab.
Yellowfin Sole |
|
Walleye pollock |
|
Red King Crab |
And we are going to estimate the indicies of these species Over the eastern and northern Bering Sea shelf.
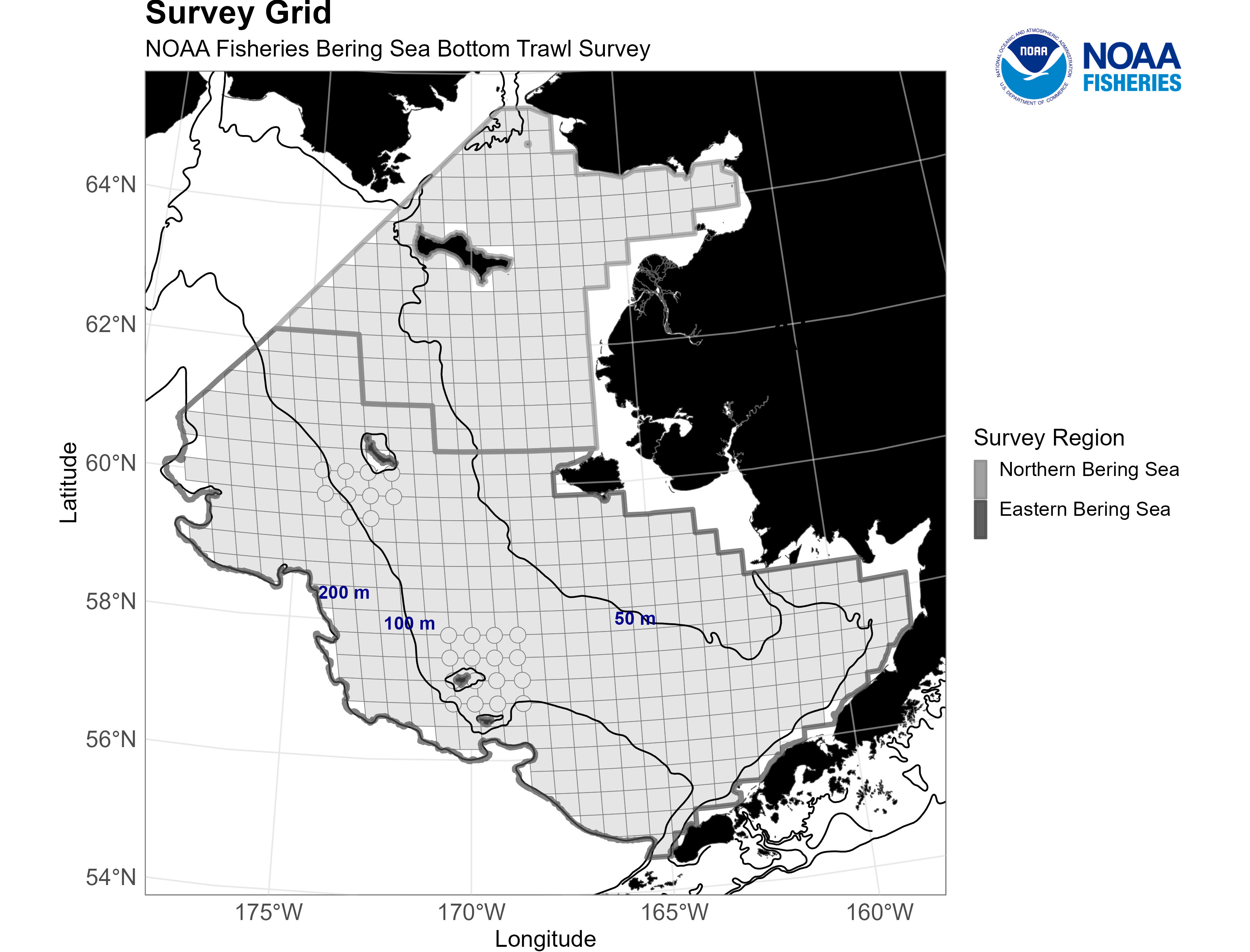
The grid of designated stations in the eastern Bering Sea and northern Bering Sea bottom trawl survey areas as well as the 50m, 100m, and 200m bathymetric boundaries. Credit: NOAA Fisheries
For the sake of a simple example, we will only assess data from 2015 to 2021.
SPECIES <- c("yellowfin sole", "walleye pollock", "red king crab")
YEARS <- 2015:2023
SRVY <- "EBS"1. What data area we using?
Here, we use the public facing data from the NOAA AFSC groundfish Bering sea bottom trawl survey. For more information about how these data were compiled, see afsc-gap-products GitHub repo.
dat <- sdmgamindex::noaa_afsc_public_foss %>%
dplyr::filter(srvy == SRVY &
year %in% YEARS &
common_name %in% SPECIES) %>%
dplyr::mutate(hauljoin = paste0(stratum, "_", station, "_", date_time)) %>%
dplyr::select(
year, date_time, latitude_dd_start, longitude_dd_start, # spatiotemproal data
cpue_kgkm2, common_name, # catch data
bottom_temperature_c, depth_m, # possible covariate data
srvy, area_swept_km2, duration_hr, vessel_id, hauljoin # haul/effort data)
)
table(dat$common_name)
#>
#> red king crab walleye pollock yellowfin sole
#> 3008 3008 3008
head(dat)
#> year date_time latitude_dd_start longitude_dd_start cpue_kgkm2
#> 1 2023 2023-07-09 07:27:45 56.65940 -171.3599 0.00000
#> 2 2023 2023-07-09 07:51:03 56.99770 -173.2508 0.00000
#> 3 2023 2023-07-01 07:06:31 57.67576 -170.2871 419.72701
#> 4 2023 2023-06-18 12:58:27 58.00859 -166.5287 79.13648
#> 5 2022 2022-07-24 07:39:26 60.02075 -176.7193 0.00000
#> 6 2022 2022-07-23 16:59:28 59.32891 -177.0694 0.00000
#> common_name bottom_temperature_c depth_m srvy area_swept_km2 duration_hr
#> 1 red king crab 4.1 119 EBS 0.049888 0.504
#> 2 red king crab 4.0 142 EBS 0.049980 0.509
#> 3 red king crab 2.3 73 EBS 0.049842 0.515
#> 4 red king crab 0.3 61 EBS 0.049939 0.530
#> 5 red king crab 2.0 141 EBS 0.052054 0.548
#> 6 red king crab 2.9 150 EBS 0.054499 0.539
#> vessel_id hauljoin
#> 1 134 61_F-23_2023-07-09 07:27:45
#> 2 162 61_G-26_2023-07-09 07:51:03
#> 3 134 42_I-21_2023-07-01 07:06:31
#> 4 134 31_J-03_2023-06-18 12:58:27
#> 5 94 61_P-30_2022-07-24 07:39:26
#> 6 162 61_N-31_2022-07-23 16:59:28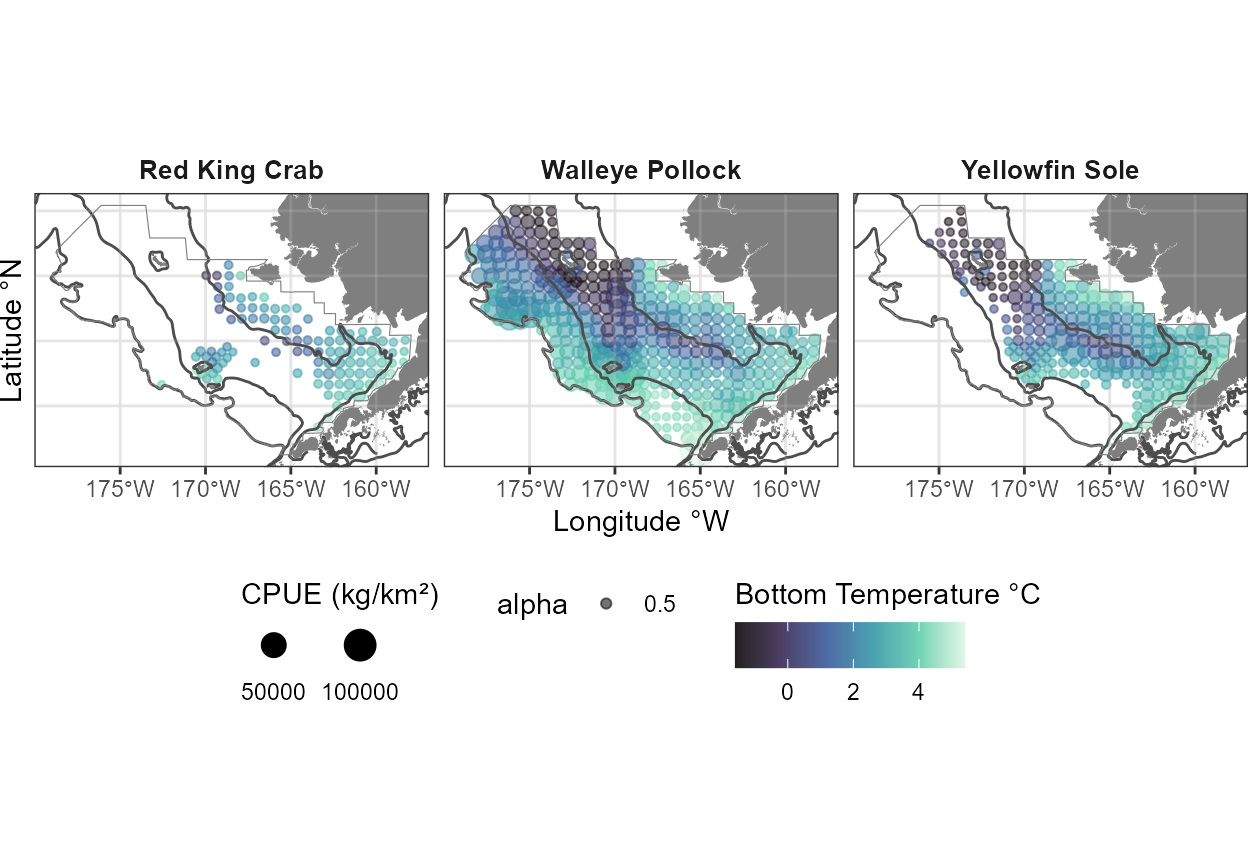
2023 species distribution relative densities (size) and bottom temperature (color).
2. Prepare the data from sdmgamindex::get_surveyidx():
# project spatial data
crs_proj <- "EPSG:3338" # NAD83 / Alaska Albers
crs_latlon <- "+proj=longlat +datum=WGS84" # decimal degrees
ll <- sdmgamindex::convert_crs(
x = dat$longitude_dd_start,
y = dat$latitude_dd_start,
crs_in = crs_latlon,
crs_out = crs_proj)
YEARS <- sort(unique(dat$year))
# The sdmgamindex::get_surveyidx() expects some columns to be named in a specific way
dat_wrangled <- dat %>%
dplyr::rename(
Year = year,
wCPUE = cpue_kgkm2,
COMMON_NAME = common_name,
GEAR_TEMPERATURE = bottom_temperature_c,
BOTTOM_DEPTH = depth_m,
HaulDur = duration_hr,
EFFORT = area_swept_km2,
Ship = vessel_id) %>%
dplyr::mutate(
# create some other vars
Lon = longitude_dd_start,
Lat = latitude_dd_start,
lon = ll$X,
lat = ll$Y,
sx = ((longitude_dd_start - mean(longitude_dd_start, na.rm = TRUE))/1000),
sy = ((latitude_dd_start - mean(latitude_dd_start, na.rm = TRUE))/1000),
ctime = as.numeric(as.character(Year)),
date_time = as.Date(x = date_time, format = "%m/%d/%Y %H:%M:%S"),
hour = as.numeric(format(date_time,"%H")),
minute = as.numeric(format(date_time,"%M")),
day = as.numeric(format(date_time,"%d")),
month = as.numeric(format(date_time,"%m")),
TimeShotHour = hour + minute/60,
timeOfYear = (month - 1) * 1/12 + (day - 1)/365,
# add some dummy vars and create some other vars
Country = "USA",
Gear = "dummy",
Quarter = "2") %>%
dplyr::mutate(across((c("Year", "Ship", "COMMON_NAME")), as.factor)) %>%
dplyr::select(wCPUE, GEAR_TEMPERATURE, BOTTOM_DEPTH, COMMON_NAME, EFFORT,
Year, Ship, Lon, Lat, lat, lon, sx, sy,
ctime, TimeShotHour, timeOfYear, Gear, Quarter, HaulDur, hauljoin)
head(dat_wrangled)
#> wCPUE GEAR_TEMPERATURE BOTTOM_DEPTH COMMON_NAME EFFORT Year Ship
#> 1 0.00000 4.1 119 red king crab 0.049888 2023 134
#> 2 0.00000 4.0 142 red king crab 0.049980 2023 162
#> 3 419.72701 2.3 73 red king crab 0.049842 2023 134
#> 4 79.13648 0.3 61 red king crab 0.049939 2023 134
#> 5 0.00000 2.0 141 red king crab 0.052054 2022 94
#> 6 0.00000 2.9 150 red king crab 0.054499 2022 162
#> Lon Lat lat lon sx sy ctime
#> 1 -171.3599 56.65940 877146.6 -1050529.3 -0.002601332 -0.0016013454 2023
#> 2 -173.2508 56.99770 944820.3 -1151106.0 -0.004492212 -0.0012630454 2023
#> 3 -170.2871 57.67576 970747.6 -959416.2 -0.001528562 -0.0005849854 2023
#> 4 -166.5287 58.00859 959133.7 -734085.4 0.002229868 -0.0002521554 2023
#> 5 -176.7193 60.02075 1328406.2 -1237677.9 -0.007960682 0.0017600046 2022
#> 6 -177.0694 59.32891 1262236.5 -1282319.2 -0.008310772 0.0010681646 2022
#> TimeShotHour timeOfYear Gear Quarter HaulDur hauljoin
#> 1 0 0.5219178 dummy 2 0.504 61_F-23_2023-07-09 07:27:45
#> 2 0 0.5219178 dummy 2 0.509 61_G-26_2023-07-09 07:51:03
#> 3 0 0.5000000 dummy 2 0.515 42_I-21_2023-07-01 07:06:31
#> 4 0 0.4632420 dummy 2 0.530 31_J-03_2023-06-18 12:58:27
#> 5 0 0.5630137 dummy 2 0.548 61_P-30_2022-07-24 07:39:26
#> 6 0 0.5602740 dummy 2 0.539 61_N-31_2022-07-23 16:59:283. Define representitive station points to fit and predict the model at
Since surveys are not done at the same exact location each year (it’s the intention, but impossible in practice), we need to define what representative latitudes and longitudes we are going to predict at.
These are the same prediction grids AFSC uses for their 2021 VAST model-based indices (which is subject to change - do not use this without asking/checking that this is still current!).
pred_grid <- sdmgamindex::pred_grid_ebs
ll <- sdmgamindex::convert_crs(
x = pred_grid$lon,
y = pred_grid$lat,
crs_in = crs_latlon,
crs_out = crs_proj)
pred_grid <- pred_grid %>%
dplyr::mutate(
lon = ll$X,
lat = ll$Y,
sx = ((lon - mean(lon, na.rm = TRUE))/1000),
sy = ((lat - mean(lat, na.rm = TRUE))/1000))
head(pred_grid)
#> # A tibble: 6 × 5
#> lon lat Shape_Area sx sy
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 -1133214. 1542340. 2449160. -290. 517.
#> 2 -1129510. 1542340. 9298535. -287. 517.
#> 3 -1125806. 1542340. 9749166. -283. 517.
#> 4 -1122102. 1542340. 5383834. -279. 517.
#> 5 -1118398. 1542340. 1173734. -275. 517.
#> 6 -1140622. 1538636. 1525663. -298. 513.It is also good to have a shapefile on hand to crop and constrain your outputs too. Here at AFSC GAP, we have developed the {akgfmaps} R package to save and share such shapefiles.
# library(devtools)
# devtools::install_github("afsc-gap-products/akgfmaps", build_vignettes = TRUE)
library(akgfmaps)
map_layers <- akgfmaps::get_base_layers(
select.region = "bs.south",
set.crs = crs_proj)
# Let's just see what that looks like:
tmp <- map_layers$survey.area
tmp$AREA_KM2 <- tmp$PERIM_KM <- NULL
plot(tmp)
4. Prepare covariate data
Here we want to match covariate data to the prediction grid.
dat_cov <- sdmgamindex::pred_grid_ebs %>%
dplyr::select(-Shape_Area) %>%
dplyr::mutate(
sx = ((lon - mean(lon, na.rm = TRUE))/1000),
sy = ((lat - mean(lat, na.rm = TRUE))/1000))
sp_extrap_raster <- SpatialPoints(
coords = coordinates(as.matrix(dat_cov[,c("lon", "lat")])),
proj4string = CRS(crs_latlon) )
dat_cov
#> # A tibble: 36,690 × 4
#> lon lat sx sy
#> <dbl> <dbl> <dbl> <dbl>
#> 1 -176. 62.1 -0.00748 0.00384
#> 2 -176. 62.1 -0.00741 0.00385
#> 3 -176. 62.2 -0.00735 0.00386
#> 4 -176. 62.2 -0.00728 0.00387
#> 5 -176. 62.2 -0.00721 0.00389
#> 6 -176. 62.1 -0.00759 0.00379
#> 7 -176. 62.1 -0.00752 0.00380
#> 8 -176. 62.1 -0.00746 0.00381
#> 9 -176. 62.1 -0.00739 0.00382
#> 10 -176. 62.1 -0.00732 0.00383
#> # ℹ 36,680 more rows
sp_extrap_raster
#> class : SpatialPoints
#> features : 36690
#> extent : -178.9664, -157.9516, 54.48348, 62.19158 (xmin, xmax, ymin, ymax)
#> crs : +proj=longlat +datum=WGS84 +no_defs4a. Data that varies over only space (depth)
Here in the Bering sea, the depth rarely changes. The modeler may consider making this variable time-varying as well if they are say, in the Gulf of Alaska or the Aleutian Islands where currents and island formation can markedly change depth.
For this, we are going to create a raster of depth in the Bering sea from the survey data so we can merge that into the dataset at the prediction grid lat/lons.
x <- dat_wrangled %>%
dplyr::select(Lon, Lat, BOTTOM_DEPTH) %>%
stats::na.omit() %>%
sf::st_as_sf(x = .,
coords = c(x = "Lon", y = "Lat"),
crs = sf::st_crs(crs_latlon))
idw_fit <- gstat::gstat(formula = BOTTOM_DEPTH ~ 1,
locations = x,
nmax = 4)
# stn_predict <- raster::predict(idw_fit, x)
extrap_data0 <- raster::predict(
idw_fit, sp_extrap_raster) %>%
# as(sp_extrap_raster, Class = "SpatialPoints")) %>%
sf::st_as_sf() %>%
sf::st_transform(crs = crs_latlon) %>%
stars::st_rasterize()
extrap_data <- stars::st_extract(x = extrap_data0,
at = as.matrix(dat_cov[,c("lon", "lat")]))
# to make future runs of this faster:
save(extrap_data0, extrap_data,
file = here::here("inst",
paste0("vigD_bottom_depth_raster_",
min(YEARS),"-",max(YEARS), ".rdata")))
# Just so we can see what we are looking at:
plot(extrap_data0, main = "Interpolated Bottom Depths") 
dat_cov <- cbind.data.frame(dat_cov,
"BOTTOM_DEPTH" = extrap_data$var1.pred) %>%
stats::na.omit()
head(dat_cov)
#> lon lat sx sy BOTTOM_DEPTH
#> 1 -176.2068 62.13518 -0.007481089 0.003842524 93.00000
#> 2 -176.1395 62.14603 -0.007413772 0.003853379 93.00000
#> 3 -176.0722 62.15686 -0.007346407 0.003864203 93.00000
#> 4 -176.0047 62.16765 -0.007278995 0.003874995 92.76145
#> 5 -175.9373 62.17841 -0.007211535 0.003885756 92.75523
#> 6 -176.3179 62.08210 -0.007592106 0.003789448 93.000004b. Data that varies over space and time (bottom temperature)
Here, bottom temperature, and thereby the cold pool extent, have been show to drive the distribution of many species. This is especially true for walleye pollock.
For this we are going to lean on our in-house prepared validated and pre-prepared {coldpool} R package [@RohanColdPool]. This data interpolates over the whole area of the survey so there are no missing data.
# Just so we can see what we are looking at:
#plot(terra::unwrap(coldpool::ebs_bottom_temperature))
tmp <- which(readr::parse_number(names(terra::unwrap(coldpool::ebs_bottom_temperature))) %in% YEARS)
dat_temperature <- terra::unwrap(coldpool::ebs_bottom_temperature)[[tmp]] %>%
terra::extract(y = dat_cov[,c("lon", "lat")] %>%
sf::sf_project(from = "+proj=longlat",
to = "EPSG:3338")) %>%
data.frame()
names(dat_temperature) <- paste0("GEAR_TEMPERATURE", YEARS)
dat_cov <- dplyr::bind_cols(dat_cov, dat_temperature) %>%
na.omit()
head(dat_cov)
#> lon lat sx sy BOTTOM_DEPTH GEAR_TEMPERATURE2015
#> 2 -176.1395 62.14603 -0.007413772 0.003853379 93.00000 -0.07311002
#> 3 -176.0722 62.15686 -0.007346407 0.003864203 93.00000 -0.07311002
#> 4 -176.0047 62.16765 -0.007278995 0.003874995 92.76145 -0.15166534
#> 7 -176.2507 62.09301 -0.007524943 0.003800355 93.00000 0.06603578
#> 8 -176.1835 62.10389 -0.007457733 0.003811231 93.00000 -0.02377643
#> 9 -176.1162 62.11473 -0.007390475 0.003822076 93.00000 -0.11071504
#> GEAR_TEMPERATURE2016 GEAR_TEMPERATURE2017 GEAR_TEMPERATURE2018
#> 2 -0.30315974 0.2442329 2.066675
#> 3 -0.30315974 0.2442329 2.066675
#> 4 -0.40172631 0.1406713 2.046152
#> 7 -0.08488923 0.4213759 2.109732
#> 8 -0.18901448 0.3380764 2.087453
#> 9 -0.29478970 0.2444835 2.064520
#> GEAR_TEMPERATURE2019 GEAR_TEMPERATURE2021 GEAR_TEMPERATURE2022
#> 2 1.242070 0.1678221 -1.1127377
#> 3 1.242070 0.1678221 -1.1127377
#> 4 1.178158 0.1119230 -1.1903751
#> 7 1.372879 0.3057251 -0.9713215
#> 8 1.317465 0.2446349 -1.0861878
#> 9 1.257273 0.1832289 -1.1890295
#> GEAR_TEMPERATURE2023
#> 2 -0.9886659
#> 3 -0.9886659
#> 4 -1.0962228
#> 7 -0.7410921
#> 8 -0.8782412
#> 9 -1.01146855. DATRAS structure
5a. Catch Data
# Identify vars that will be used --------------------------------------------
varsbyyr <- unique( # c("GEAR_TEMPERATURE", "cpi")
gsub(pattern = "[0-9]+",
replacement = "",
x = names(dat_cov)[grepl(names(dat_cov),
pattern = "[0-9]+")]))
vars <- unique( # c("BOTTOM_DEPTH")
names(dat_cov)[!grepl(names(dat_cov),
pattern = "[0-9]+")])
vars <- vars[!(vars %in% c("LONG", "LAT", "lon", "lat", "sx", "sy"))]
dat_catch_haul <- dat_wrangled
head(dat_catch_haul)
#> wCPUE GEAR_TEMPERATURE BOTTOM_DEPTH COMMON_NAME EFFORT Year Ship
#> 1 0.00000 4.1 119 red king crab 0.049888 2023 134
#> 2 0.00000 4.0 142 red king crab 0.049980 2023 162
#> 3 419.72701 2.3 73 red king crab 0.049842 2023 134
#> 4 79.13648 0.3 61 red king crab 0.049939 2023 134
#> 5 0.00000 2.0 141 red king crab 0.052054 2022 94
#> 6 0.00000 2.9 150 red king crab 0.054499 2022 162
#> Lon Lat lat lon sx sy ctime
#> 1 -171.3599 56.65940 877146.6 -1050529.3 -0.002601332 -0.0016013454 2023
#> 2 -173.2508 56.99770 944820.3 -1151106.0 -0.004492212 -0.0012630454 2023
#> 3 -170.2871 57.67576 970747.6 -959416.2 -0.001528562 -0.0005849854 2023
#> 4 -166.5287 58.00859 959133.7 -734085.4 0.002229868 -0.0002521554 2023
#> 5 -176.7193 60.02075 1328406.2 -1237677.9 -0.007960682 0.0017600046 2022
#> 6 -177.0694 59.32891 1262236.5 -1282319.2 -0.008310772 0.0010681646 2022
#> TimeShotHour timeOfYear Gear Quarter HaulDur hauljoin
#> 1 0 0.5219178 dummy 2 0.504 61_F-23_2023-07-09 07:27:45
#> 2 0 0.5219178 dummy 2 0.509 61_G-26_2023-07-09 07:51:03
#> 3 0 0.5000000 dummy 2 0.515 42_I-21_2023-07-01 07:06:31
#> 4 0 0.4632420 dummy 2 0.530 31_J-03_2023-06-18 12:58:27
#> 5 0 0.5630137 dummy 2 0.548 61_P-30_2022-07-24 07:39:26
#> 6 0 0.5602740 dummy 2 0.539 61_N-31_2022-07-23 16:59:28
allpd <- lapply(YEARS,
FUN = sdmgamindex::get_prediction_grid,
x = dat_cov,
vars = vars,
varsbyyr = varsbyyr)
names(allpd) <- as.character(YEARS)
head(allpd[1][[1]])
#> lon lat sx sy BOTTOM_DEPTH GEAR_TEMPERATURE
#> 2 -176.1395 62.14603 -0.007413772 0.003853379 93.00000 -0.07311002
#> 3 -176.0722 62.15686 -0.007346407 0.003864203 93.00000 -0.07311002
#> 4 -176.0047 62.16765 -0.007278995 0.003874995 92.76145 -0.15166534
#> 7 -176.2507 62.09301 -0.007524943 0.003800355 93.00000 0.06603578
#> 8 -176.1835 62.10389 -0.007457733 0.003811231 93.00000 -0.02377643
#> 9 -176.1162 62.11473 -0.007390475 0.003822076 93.00000 -0.11071504
#> EFFORT
#> 2 1
#> 3 1
#> 4 1
#> 7 1
#> 8 1
#> 9 15b. Covariate Data
## split data by species, make into DATRASraw + Nage matrix
ds <- split(dat_catch_haul,dat_catch_haul$COMMON_NAME)
ds <- lapply(ds, sdmgamindex::get_datrasraw)
## OBS, response is added here in "Nage" matrix -- use wCPUE
ds <- lapply(ds,function(x) { x[[2]]$Nage <- matrix(x$wCPUE,ncol=1); colnames(x[[2]]$Nage)<-1; x } )
save(ds, file = here::here("inst",paste0("vigD_DATRAS.Rdata")))
ds
#> $`red king crab`
#> Object of class 'DATRASraw'
#> ===========================
#> Number of hauls: 3008
#> Number of species: 0
#> Number of countries: 0
#> Years: 2015 2016 2017 2018 2019 2021 2022 2023
#> Quarters:
#> Gears:
#> Haul duration: 0.189 - 0.656 minutes
#>
#> $`walleye pollock`
#> Object of class 'DATRASraw'
#> ===========================
#> Number of hauls: 3008
#> Number of species: 0
#> Number of countries: 0
#> Years: 2015 2016 2017 2018 2019 2021 2022 2023
#> Quarters:
#> Gears:
#> Haul duration: 0.189 - 0.656 minutes
#>
#> $`yellowfin sole`
#> Object of class 'DATRASraw'
#> ===========================
#> Number of hauls: 3008
#> Number of species: 0
#> Number of countries: 0
#> Years: 2015 2016 2017 2018 2019 2021 2022 2023
#> Quarters:
#> Gears:
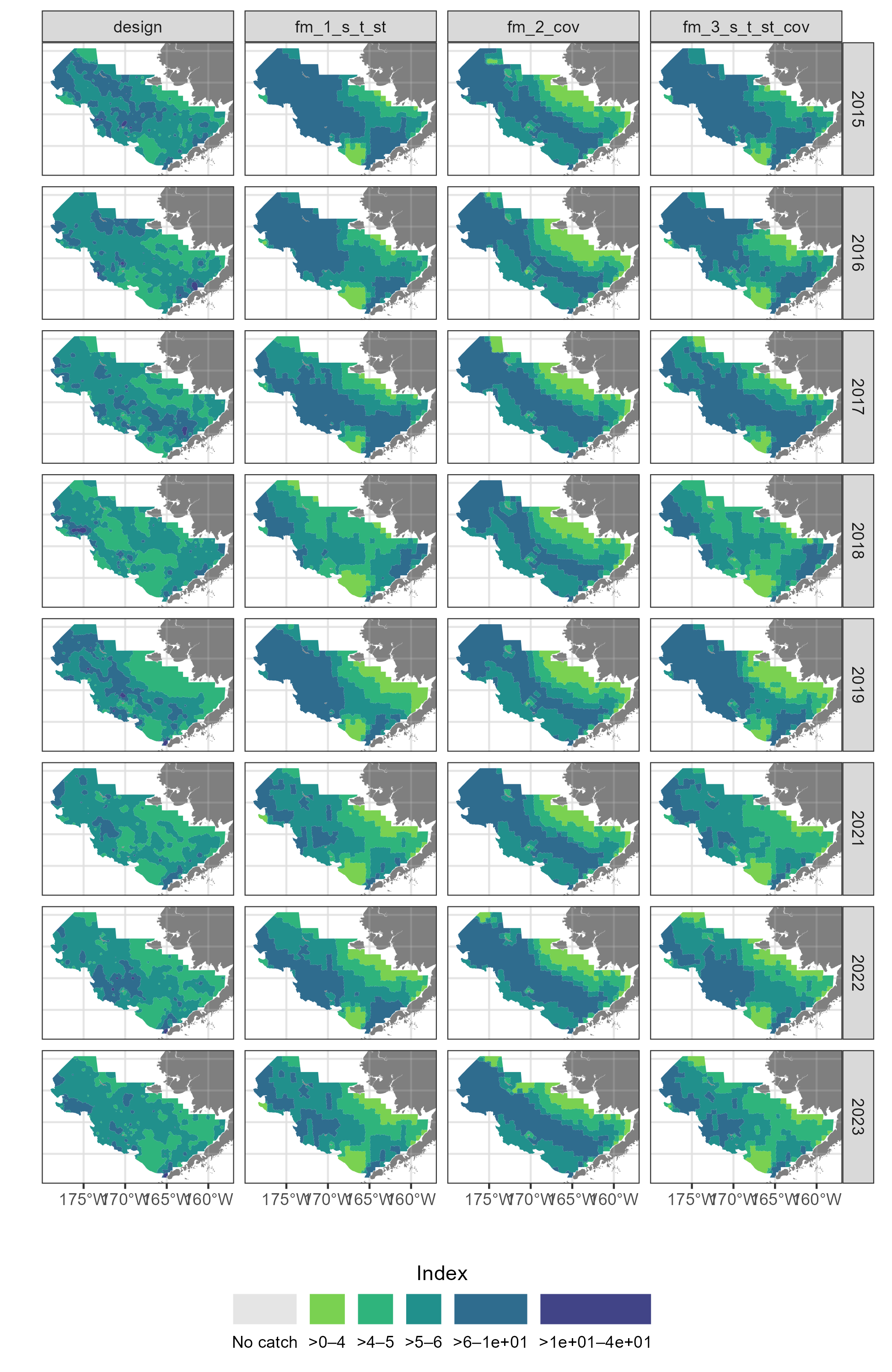
#> Haul duration: 0.189 - 0.656 minutes6. Formulas
fm <- list(
# Null model spatial and temporal with an additional year effect
"fm_1_s_t_st" =
"Year +
s(sx,sy,bs=c('ts'),k=376) +
s(sx,sy,bs=c('ts'),k=10,by=Year)",
# Mdoel with simple covariates
"fm_2_cov" =
"s(BOTTOM_DEPTH,bs='ts',k=10) +
s(log(GEAR_TEMPERATURE+3),bs='ts',k=10)",
# Mdoel with simple covariates and spatial and temporal with an additional year effect
"fm_3_s_t_st_cov" =
"Year +
s(sx,sy,bs=c('ts'),k=376) +
s(sx,sy,bs=c('ts'),k=10,by=Year) +
s(BOTTOM_DEPTH,bs='ts',k=10) +
s(log(GEAR_TEMPERATURE+3),bs='ts',k=10)" )7. Fit the Model
Here are all of the models we want to try fitting:
models <- fittimes <- list()
for(i in 1:nrow(comb)){
cat("Fitting ",comb$SPECIES[i],"\n", comb$fm_name[i], ": ", comb$fm[i], "\n")
temp <- paste0(comb$SPECIES[i], " ", comb$fm_name[i])
fittimes[[ temp ]] <-
system.time ( models[[ temp ]] <-
sdmgamindex::get_surveyidx(
x = ds[[ comb$SPECIES[i] ]],
ages = 1,
myids = NULL,
predD = allpd,
cutOff = 0,
fam = "Tweedie",
modelP = comb$fm[i],
gamma = 1,
control = list(trace = TRUE,
maxit = 20)) )
model <- models[[ temp ]]
fittime <- fittimes[[ temp ]]
save(model, fittime, file = here::here("inst",paste0("vigD_model_fits_",comb$SPECIES[i], "_", comb$fm_name[i],".Rdata")))
}#>
#> red king crab fm_1_s_t_st: 1.3e+03 minutes
#> red king crab fm_2_cov: 41 minutes
#> red king crab fm_3_s_t_st_cov: 1.6e+03 minutes
#> walleye pollock fm_1_s_t_st: 1.7e+03 minutes
#> walleye pollock fm_2_cov: 40 minutes
#> walleye pollock fm_3_s_t_st_cov: 1.8e+03 minutes
#> yellowfin sole fm_1_s_t_st: 1.4e+03 minutes
#> yellowfin sole fm_2_cov: 41 minutes
#> yellowfin sole fm_3_s_t_st_cov: 1.4e+03 minutes
# AIC(sapply(sapply(models,"[[",'pModels'),"[[",1))
# sdmgamindex::get_surveyidx_aic(x = models)
aic <- AIC(
models$`red king crab fm_1_s_t_st`$pModels[[1]],
models$`red king crab fm_2_cov`$pModels[[1]],
models$`red king crab fm_3_s_t_st_cov`$pModels[[1]],
models$`walleye pollock fm_1_s_t_st`$pModels[[1]],
models$`walleye pollock fm_2_cov`$pModels[[1]],
models$`walleye pollock fm_3_s_t_st_cov`$pModels[[1]],
models$`yellowfin sole fm_1_s_t_st`$pModels[[1]],
models$`yellowfin sole fm_2_cov`$pModels[[1]],
models$`yellowfin sole fm_3_s_t_st_cov`$pModels[[1]])
aic %>%
tibble::rownames_to_column("model") %>%
dplyr::mutate(model = gsub(pattern = "models$`", replacement = "", x = model, fixed = TRUE),
model = gsub(pattern = "`$pModels[[1]]", replacement = "", x = model, fixed = TRUE)) %>%
tidyr::separate(col = model, into = c("SPECIES", "fm"), sep = " fm_") %>%
dplyr::group_by(SPECIES) %>%
dplyr::mutate(dAIC = round(AIC-min(AIC), digits = 2)) %>%
dplyr::ungroup() %>%
flextable::flextable() %>%
# flextable::merge_at(i = SPECIES, part = "body") %>%
flextable::width(j = "SPECIES", width = 1, unit = "in") SPECIES |
fm |
df |
AIC |
dAIC |
|---|---|---|---|---|
red king crab |
1_s_t_st |
154.49858 |
12,311.62 |
83.39 |
red king crab |
2_cov |
16.90395 |
13,568.53 |
1,340.29 |
red king crab |
3_s_t_st_cov |
156.75224 |
12,228.24 |
0.00 |
walleye pollock |
1_s_t_st |
197.59827 |
58,792.61 |
242.24 |
walleye pollock |
2_cov |
18.36274 |
59,795.46 |
1,245.09 |
walleye pollock |
3_s_t_st_cov |
216.42478 |
58,550.37 |
0.00 |
yellowfin sole |
1_s_t_st |
238.72208 |
36,516.28 |
115.22 |
yellowfin sole |
2_cov |
16.24816 |
38,060.37 |
1,659.31 |
yellowfin sole |
3_s_t_st_cov |
202.01411 |
36,401.06 |
0.00 |
## Model summaries
lapply(models,function(x) summary(x$pModels[[1]]))
#> $`red king crab fm_1_s_t_st`
#>
#> Family: Tweedie(p=1.446)
#> Link function: log
#>
#> Formula:
#> A1 ~ Year + s(sx, sy, bs = c("ts"), k = 376) + s(sx, sy, bs = c("ts"),
#> k = 10, by = Year)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.98012 1.25695 -1.575 0.1153
#> Year2016 -0.26703 0.23477 -1.137 0.2555
#> Year2017 0.01753 0.20073 0.087 0.9304
#> Year2018 -0.43054 0.20678 -2.082 0.0374 *
#> Year2019 -0.07056 0.38366 -0.184 0.8541
#> Year2021 0.33813 0.21900 1.544 0.1227
#> Year2022 0.18401 0.21417 0.859 0.3903
#> Year2023 -0.14346 0.20276 -0.708 0.4793
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(sx,sy) 129.3276662 375 4.974 < 0.0000000000000002 ***
#> s(sx,sy):Year2015 1.9324308 9 4.208 < 0.0000000000000002 ***
#> s(sx,sy):Year2016 1.8720437 9 2.599 0.00000294 ***
#> s(sx,sy):Year2017 0.0009186 9 0.000 0.271236
#> s(sx,sy):Year2018 0.0008940 9 0.000 0.505286
#> s(sx,sy):Year2019 3.6437459 9 1.880 0.000612 ***
#> s(sx,sy):Year2021 1.7831412 9 2.353 0.00000607 ***
#> s(sx,sy):Year2022 1.0083459 9 0.337 0.049150 *
#> s(sx,sy):Year2023 0.0002364 9 0.000 0.574074
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.383 Deviance explained = 80.9%
#> -ML = 6254 Scale est. = 24.547 n = 3008
#>
#> $`red king crab fm_2_cov`
#>
#> Family: Tweedie(p=1.551)
#> Link function: log
#>
#> Formula:
#> A1 ~ s(BOTTOM_DEPTH, bs = "ts", k = 10) + s(log(GEAR_TEMPERATURE +
#> 3), bs = "ts", k = 10)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.8184 0.3276 2.498 0.0125 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(BOTTOM_DEPTH) 6.032 9 64.85 <0.0000000000000002 ***
#> s(log(GEAR_TEMPERATURE + 3)) 6.533 9 33.04 <0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.0909 Deviance explained = 49.8%
#> -ML = 6806.2 Scale est. = 33.425 n = 3008
#>
#> $`red king crab fm_3_s_t_st_cov`
#>
#> Family: Tweedie(p=1.433)
#> Link function: log
#>
#> Formula:
#> A1 ~ Year + s(sx, sy, bs = c("ts"), k = 376) + s(sx, sy, bs = c("ts"),
#> k = 10, by = Year) + s(BOTTOM_DEPTH, bs = "ts", k = 10) +
#> s(log(GEAR_TEMPERATURE + 3), bs = "ts", k = 10)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.2071 1.2522 -0.964 0.335
#> Year2016 -0.8059 0.9654 -0.835 0.404
#> Year2017 -1.3099 0.9539 -1.373 0.170
#> Year2018 -1.5325 0.9558 -1.603 0.109
#> Year2019 -0.8059 1.0276 -0.784 0.433
#> Year2021 -0.9672 0.9580 -1.010 0.313
#> Year2022 -1.1494 0.9578 -1.200 0.230
#> Year2023 -1.5415 0.9560 -1.612 0.107
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(sx,sy) 112.2583917 375 3.061 < 0.0000000000000002 ***
#> s(sx,sy):Year2015 6.8322604 9 9.486 < 0.0000000000000002 ***
#> s(sx,sy):Year2016 1.6506829 9 1.452 0.000303 ***
#> s(sx,sy):Year2017 0.0002462 9 0.000 0.429081
#> s(sx,sy):Year2018 0.0010538 9 0.000 0.484492
#> s(sx,sy):Year2019 4.2828597 9 2.860 0.0000132 ***
#> s(sx,sy):Year2021 1.6758276 9 1.769 0.0000654 ***
#> s(sx,sy):Year2022 1.0851801 9 0.399 0.035837 *
#> s(sx,sy):Year2023 0.0004316 9 0.000 0.423626
#> s(BOTTOM_DEPTH) 3.7496746 9 4.081 < 0.0000000000000002 ***
#> s(log(GEAR_TEMPERATURE + 3)) 5.3404899 9 8.482 < 0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.466 Deviance explained = 82.1%
#> -ML = 6222.4 Scale est. = 24.551 n = 3008
#>
#> $`walleye pollock fm_1_s_t_st`
#>
#> Family: Tweedie(p=1.852)
#> Link function: log
#>
#> Formula:
#> A1 ~ Year + s(sx, sy, bs = c("ts"), k = 376) + s(sx, sy, bs = c("ts"),
#> k = 10, by = Year)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 9.23060 0.05088 181.433 < 0.0000000000000002 ***
#> Year2016 -0.34496 0.07286 -4.734 0.000002304557164575 ***
#> Year2017 -0.25207 0.07261 -3.472 0.000525 ***
#> Year2018 -0.88267 0.07448 -11.851 < 0.0000000000000002 ***
#> Year2019 -0.41853 0.07320 -5.718 0.000000011931844893 ***
#> Year2021 -0.86765 0.07432 -11.674 < 0.0000000000000002 ***
#> Year2022 -0.60495 0.07364 -8.215 0.000000000000000319 ***
#> Year2023 -0.78230 0.07400 -10.572 < 0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(sx,sy) 166.073525 375 4.418 < 0.0000000000000002 ***
#> s(sx,sy):Year2015 0.002624 9 0.000 0.99690
#> s(sx,sy):Year2016 1.773308 9 1.107 0.00308 **
#> s(sx,sy):Year2017 1.875983 9 6.011 < 0.0000000000000002 ***
#> s(sx,sy):Year2018 7.895874 9 12.792 < 0.0000000000000002 ***
#> s(sx,sy):Year2019 1.963464 9 5.689 < 0.0000000000000002 ***
#> s(sx,sy):Year2021 1.057997 9 0.270 0.09881 .
#> s(sx,sy):Year2022 1.913812 9 3.195 0.000000625 ***
#> s(sx,sy):Year2023 0.005541 9 0.000 0.79914
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.157 Deviance explained = 40.5%
#> -ML = 29507 Scale est. = 3.8493 n = 3008
#>
#> $`walleye pollock fm_2_cov`
#>
#> Family: Tweedie(p=1.885)
#> Link function: log
#>
#> Formula:
#> A1 ~ s(BOTTOM_DEPTH, bs = "ts", k = 10) + s(log(GEAR_TEMPERATURE +
#> 3), bs = "ts", k = 10)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.98071 0.02158 416.2 <0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(BOTTOM_DEPTH) 6.340 9 33.86 <0.0000000000000002 ***
#> s(log(GEAR_TEMPERATURE + 3)) 7.483 9 12.77 <0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.0501 Deviance explained = 13.4%
#> -ML = 29917 Scale est. = 3.9341 n = 3008
#>
#> $`walleye pollock fm_3_s_t_st_cov`
#>
#> Family: Tweedie(p=1.845)
#> Link function: log
#>
#> Formula:
#> A1 ~ Year + s(sx, sy, bs = c("ts"), k = 376) + s(sx, sy, bs = c("ts"),
#> k = 10, by = Year) + s(BOTTOM_DEPTH, bs = "ts", k = 10) +
#> s(log(GEAR_TEMPERATURE + 3), bs = "ts", k = 10)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 9.28409 0.05025 184.775 < 0.0000000000000002 ***
#> Year2016 -0.10527 0.07787 -1.352 0.17651
#> Year2017 -0.54712 0.07343 -7.451 0.000000000000123 ***
#> Year2018 -0.80830 0.07761 -10.415 < 0.0000000000000002 ***
#> Year2019 -0.23379 0.07802 -2.997 0.00275 **
#> Year2021 -1.06709 0.07515 -14.199 < 0.0000000000000002 ***
#> Year2022 -0.99166 0.07624 -13.008 < 0.0000000000000002 ***
#> Year2023 -1.20438 0.07827 -15.388 < 0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(sx,sy) 163.87357 375 3.153 < 0.0000000000000002 ***
#> s(sx,sy):Year2015 0.03236 9 0.002 0.260260
#> s(sx,sy):Year2016 1.97517 9 5.699 < 0.0000000000000002 ***
#> s(sx,sy):Year2017 1.56004 9 1.230 0.000361 ***
#> s(sx,sy):Year2018 8.13378 9 14.218 < 0.0000000000000002 ***
#> s(sx,sy):Year2019 1.61099 9 0.801 0.006697 **
#> s(sx,sy):Year2021 1.29987 9 0.519 0.018928 *
#> s(sx,sy):Year2022 6.51218 9 3.296 0.0000113 ***
#> s(sx,sy):Year2023 1.61223 9 0.834 0.005508 **
#> s(BOTTOM_DEPTH) 5.42839 9 3.259 < 0.0000000000000002 ***
#> s(log(GEAR_TEMPERATURE + 3)) 6.16829 9 23.184 < 0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.194 Deviance explained = 45.1%
#> -ML = 29411 Scale est. = 3.7982 n = 3008
#>
#> $`yellowfin sole fm_1_s_t_st`
#>
#> Family: Tweedie(p=1.583)
#> Link function: log
#>
#> Formula:
#> A1 ~ Year + s(sx, sy, bs = c("ts"), k = 376) + s(sx, sy, bs = c("ts"),
#> k = 10, by = Year)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.77833 0.14960 25.256 <0.0000000000000002 ***
#> Year2016 0.94125 0.11169 8.427 <0.0000000000000002 ***
#> Year2017 1.02760 0.11113 9.247 <0.0000000000000002 ***
#> Year2018 0.98426 0.11136 8.839 <0.0000000000000002 ***
#> Year2019 1.55079 0.13805 11.233 <0.0000000000000002 ***
#> Year2021 0.07911 0.11504 0.688 0.4917
#> Year2022 0.24894 0.11536 2.158 0.0310 *
#> Year2023 -0.30006 0.11907 -2.520 0.0118 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(sx,sy) 203.387176 375 12.980 < 0.0000000000000002 ***
#> s(sx,sy):Year2015 3.355870 9 5.615 < 0.0000000000000002 ***
#> s(sx,sy):Year2016 1.956443 9 4.658 < 0.0000000000000002 ***
#> s(sx,sy):Year2017 1.963583 9 4.683 < 0.0000000000000002 ***
#> s(sx,sy):Year2018 2.015209 9 10.482 < 0.0000000000000002 ***
#> s(sx,sy):Year2019 7.347153 9 22.577 < 0.0000000000000002 ***
#> s(sx,sy):Year2021 0.003934 9 0.000 0.48971
#> s(sx,sy):Year2022 1.605472 9 0.886 0.00503 **
#> s(sx,sy):Year2023 1.351760 9 0.756 0.00561 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.479 Deviance explained = 85.6%
#> -ML = 18452 Scale est. = 17.843 n = 3008
#>
#> $`yellowfin sole fm_2_cov`
#>
#> Family: Tweedie(p=1.621)
#> Link function: log
#>
#> Formula:
#> A1 ~ s(BOTTOM_DEPTH, bs = "ts", k = 10) + s(log(GEAR_TEMPERATURE +
#> 3), bs = "ts", k = 10)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.9689 0.1311 37.91 <0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(BOTTOM_DEPTH) 5.717 9 322.67 <0.0000000000000002 ***
#> s(log(GEAR_TEMPERATURE + 3)) 7.157 9 65.97 <0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.301 Deviance explained = 69.2%
#> -ML = 19054 Scale est. = 24.209 n = 3008
#>
#> $`yellowfin sole fm_3_s_t_st_cov`
#>
#> Family: Tweedie(p=1.588)
#> Link function: log
#>
#> Formula:
#> A1 ~ Year + s(sx, sy, bs = c("ts"), k = 376) + s(sx, sy, bs = c("ts"),
#> k = 10, by = Year) + s(BOTTOM_DEPTH, bs = "ts", k = 10) +
#> s(log(GEAR_TEMPERATURE + 3), bs = "ts", k = 10)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.79038 0.14456 26.221 < 0.0000000000000002 ***
#> Year2016 0.56834 0.09456 6.010 0.00000000209 ***
#> Year2017 0.90729 0.08819 10.288 < 0.0000000000000002 ***
#> Year2018 0.58164 0.09561 6.083 0.00000000134 ***
#> Year2019 1.17479 0.13219 8.887 < 0.0000000000000002 ***
#> Year2021 -0.20346 0.09928 -2.049 0.04053 *
#> Year2022 0.12633 0.10079 1.253 0.21016
#> Year2023 -0.29181 0.10680 -2.732 0.00633 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(sx,sy) 159.2359674 375 4.277 < 0.0000000000000002 ***
#> s(sx,sy):Year2015 1.8021361 9 2.059 0.0000292 ***
#> s(sx,sy):Year2016 0.0004319 9 0.000 0.427
#> s(sx,sy):Year2017 0.0232099 9 0.003 0.329
#> s(sx,sy):Year2018 1.8392011 9 2.161 0.0000213 ***
#> s(sx,sy):Year2019 7.8978827 9 17.041 < 0.0000000000000002 ***
#> s(sx,sy):Year2021 1.9647717 9 4.986 < 0.0000000000000002 ***
#> s(sx,sy):Year2022 1.9881936 9 8.208 < 0.0000000000000002 ***
#> s(sx,sy):Year2023 1.9869675 9 7.013 < 0.0000000000000002 ***
#> s(BOTTOM_DEPTH) 5.2738584 9 17.689 < 0.0000000000000002 ***
#> s(log(GEAR_TEMPERATURE + 3)) 5.3655026 9 12.804 < 0.0000000000000002 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.49 Deviance explained = 85.8%
#> -ML = 18353 Scale est. = 16.809 n = 30088. Indicies of Abundance
dat_design <- dplyr::bind_rows(
sdmgamindex::noaa_afsc_biomass_estimates %>%
dplyr::filter(survey_definition_id == 98 &
year %in% YEARS &
species_code %in% c(21740, 10210)) %>%
dplyr::mutate(common_name = dplyr::case_when(
species_code == 21740 ~ "walleye pollock",
species_code == 10210 ~ "yellowfin sole")) %>%
dplyr::select(Year = year, Estimate_metric_tons = biomass_mt, SD_mt = biomass_var, common_name) ,
read.csv(file = system.file("RKC_Table_for_SS3.csv",
package = "sdmgamindex" )) %>%
dplyr::mutate(common_name = "red king crab") %>%
dplyr::select(-Unit, -Fleet, -SD_log)) %>%
dplyr::rename(design_mt = Estimate_metric_tons,
design_se = SD_mt) %>%
dplyr::mutate(design_se = (design_se)^2,
design_CV = NA,
VAST_mt = NA,
VAST_se = NA,
VAST_CV = NA)
dat <- data.frame()
for (i in 1:length(models)){
temp <- models[[i]]
dat0 <- data.frame(idx = temp$idx[,1]/1e2, # clearly having an issue with units
lo = temp$lo[,1]/1e2,
up = temp$up[,1]/1e2,
Year = rownames(temp$idx),
common_name = lapply(strsplit(x = names(models)[i], split = " fm"), `[[`, 1)[[1]],
group = paste0("fm", lapply(strsplit(x = names(models)[i], split = " fm"), `[[`, 2)),
formula = paste0("cpue_kgkm2 ~ ",
as.character(temp$pModels[[1]]$formula)[[3]]))
dat <- dplyr::bind_rows(dat, dat0)
}
dat <- dplyr::bind_rows(dat %>%
dplyr::mutate(Year = as.numeric(Year)), # %>%
# dplyr::select(-group),
dat_design %>%
dplyr::select(design_mt, common_name, Year) %>%
dplyr::rename(idx = design_mt) %>%
dplyr::mutate(lo = NA,
up = NA,
group = "design",
formula = "design")) %>%
dplyr::filter(Year %in% (YEARS)[-1])
# dplyr::filter(Year >= min(YEARS))
dat[dat$Year == 2020, c("idx", "up", "lo")] <- NA
figure <- ggplot2::ggplot(data = dat,
mapping = aes(x = Year,
y = idx,
group = group,
color = group)) +
ggplot2::geom_line(size = 1.5) +
ggplot2::geom_point(size = 2) +
ggplot2::geom_ribbon(aes(ymin = lo, ymax = up, fill = group, color = group),
alpha = 0.1,
linetype = "dashed") +
ggplot2::ggtitle("Annual Index Model Results") +
ggplot2::scale_y_continuous(name = "Index", labels = scales::comma) +
ggplot2::facet_wrap(vars(common_name), scales = "free_y", ncol = 1) +
ggplot2::theme(legend.position = "bottom",
legend.direction = "horizontal",
legend.title = element_blank())
ggsave(filename = paste0("vigD_model_fit_timeseries.png"),
path = here::here("vignettes"),
plot = figure,
width = 6.5, height = 6)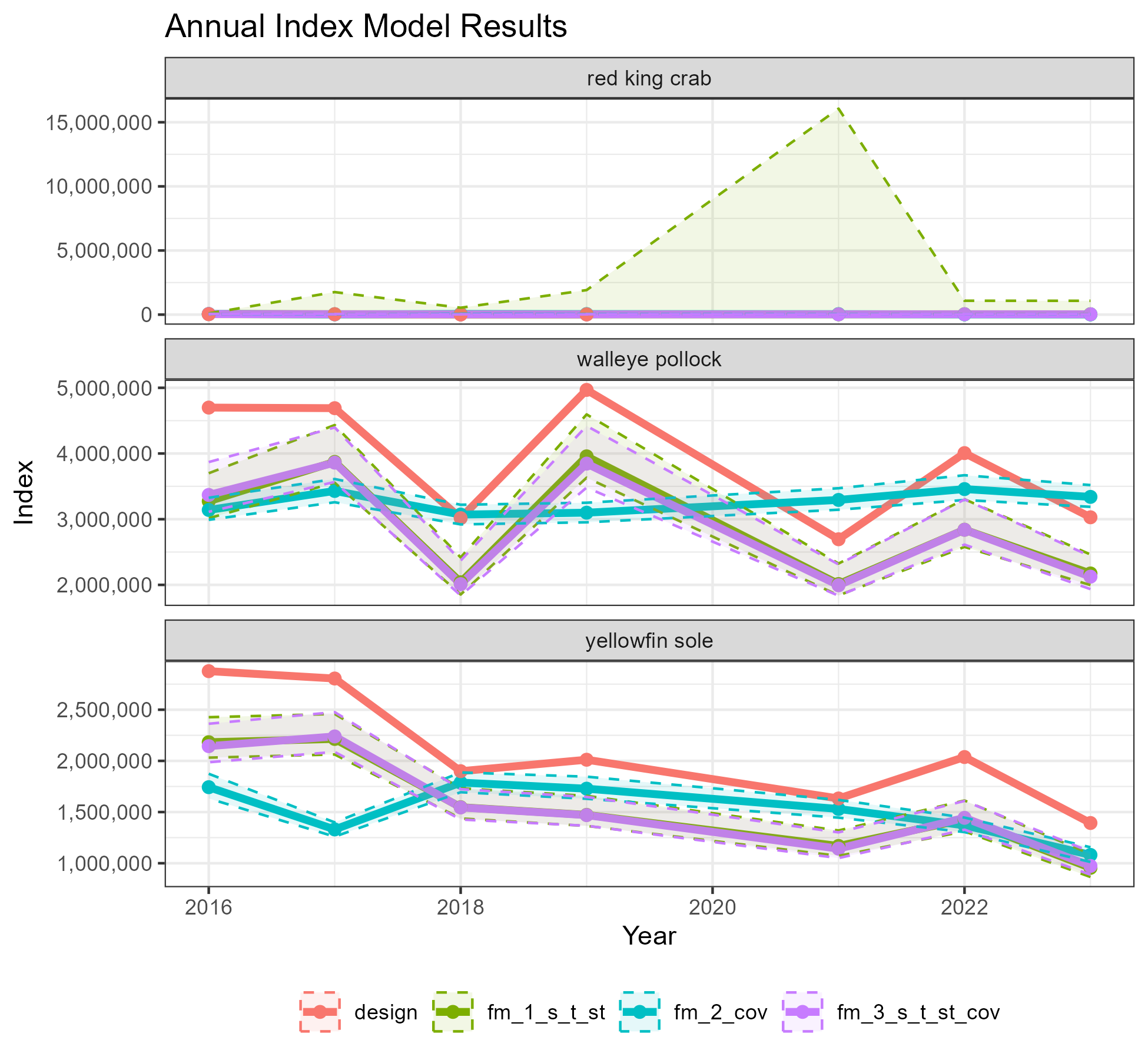
10. Simulations
sims <- fittimes <- list()
for(i in 1:nrow(comb)){
cat("Simulating ",comb$SPECIES[i],"\n", comb$fm_name[i], ": ", comb$fm[i], "\n")
temp <- paste0(comb$SPECIES[i], " ", comb$fm_name[i])
fittimes[[ temp ]] <-
system.time ( sims[[ temp ]] <-
sdmgamindex::get_surveyidx_sim(
model = models[[i]],
d = ds[[ comb$SPECIES[i] ]]) )
sim <- sims[[ temp ]]
fittime <- fittimes[[ temp ]]
save(sim, fittime, file = here::here("inst",paste0("vigD_model_sims_",comb$SPECIES[i], "_", comb$fm_name[i],".Rdata")))
}#>
#> red king crab fm_1_s_t_st: 5.3 minutes
#> red king crab fm_2_cov: 0.03 minutes
#> red king crab fm_3_s_t_st_cov: 6.2 minutes
#> walleye pollock fm_1_s_t_st: 5.3 minutes
#> walleye pollock fm_2_cov: 0.11 minutes
#> walleye pollock fm_3_s_t_st_cov: 5.4 minutes
#> yellowfin sole fm_1_s_t_st: 5.4 minutes
#> yellowfin sole fm_2_cov: 0.04 minutes
#> yellowfin sole fm_3_s_t_st_cov: 5.2 minutes
# par(mfrow = c(2, 2)) # Create a 2 x 2 plotting matrix
# for(i in 1:nrow(comb)){
# # png('output/my_plot.png')
# plot(sims[[i]]$sim, main = paste0(names(sims)[i], " sims"))
# plot(sims[[i]]$mu[[1]], main = paste0(names(sims)[i], " mu"))
# # dev.off()
# }
dat <- c()
for(i in 1:nrow(comb)){
dat <- dat %>%
dplyr::bind_rows(
data.frame(
SPECIES = comb$SPECIES[i],
model = comb$fm_name[i],
Simulations = as.vector(sims[[i]]$sim),
Mean = as.vector(sims[[i]]$mu[[1]]),
Index = 1:nrow(sims[[i]]$sim)) )
}
dat <- dat %>%
tidyr::pivot_longer(cols = c("Simulations", "Mean"), names_to = "type", values_to = "val")
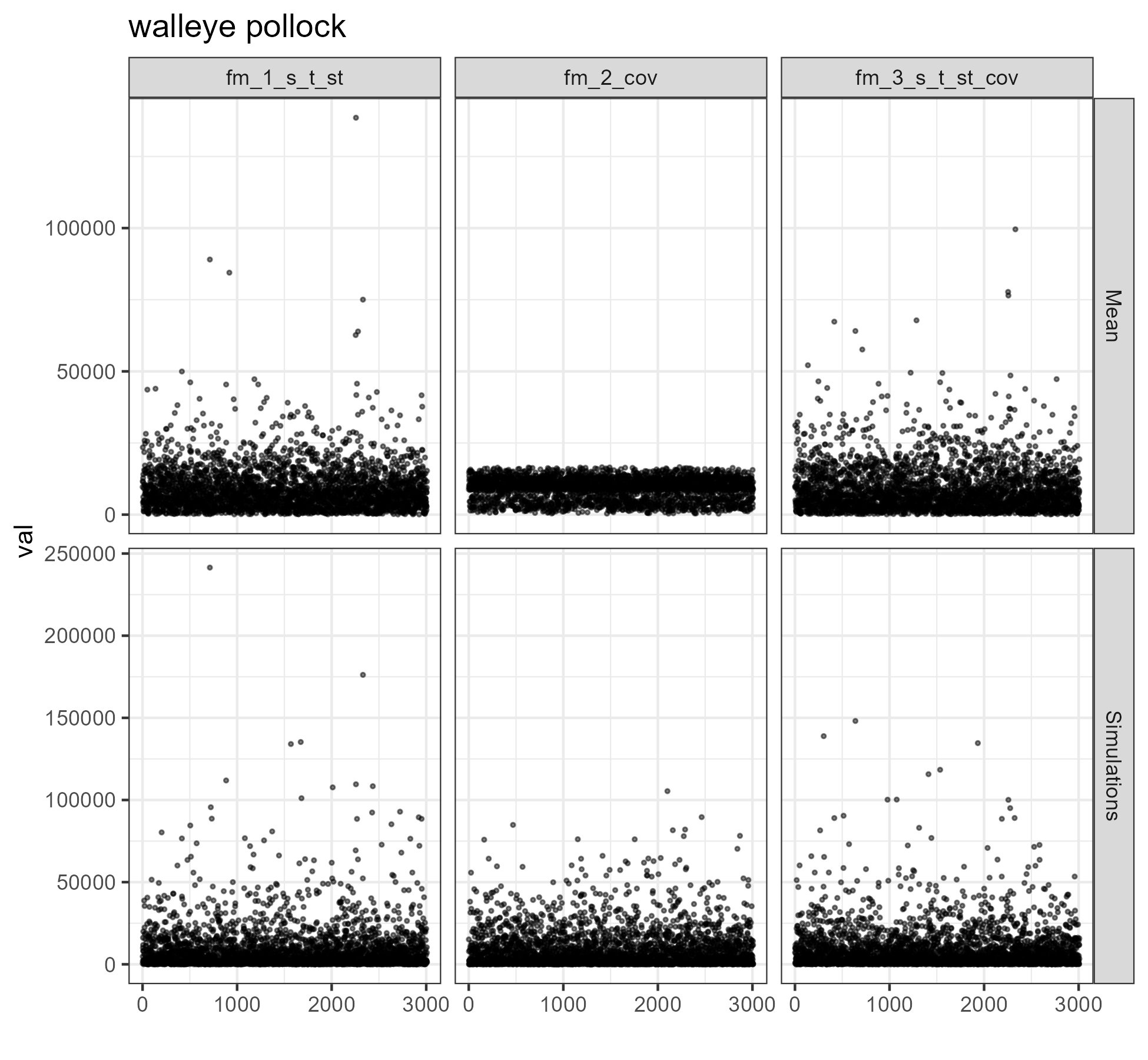
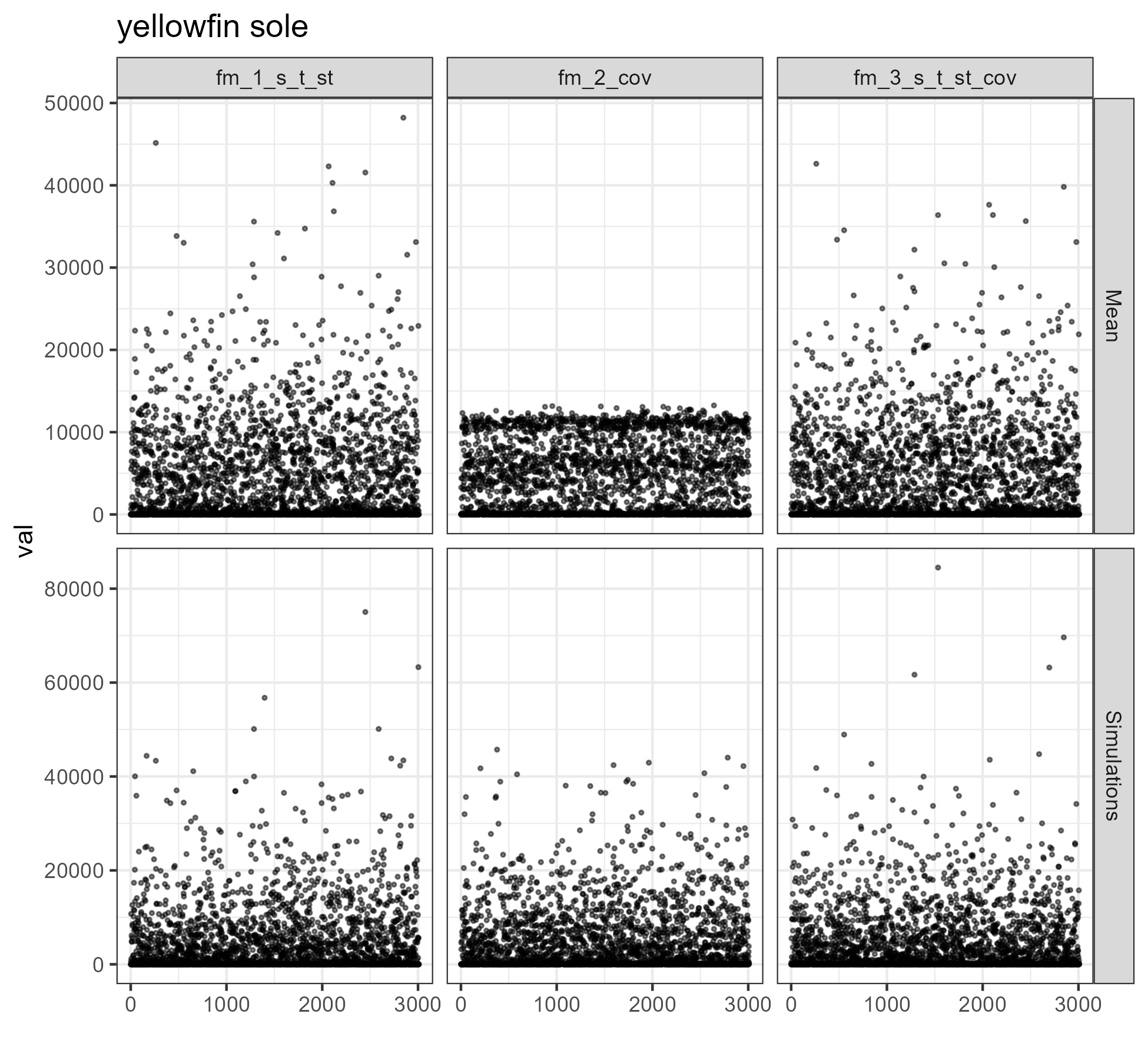
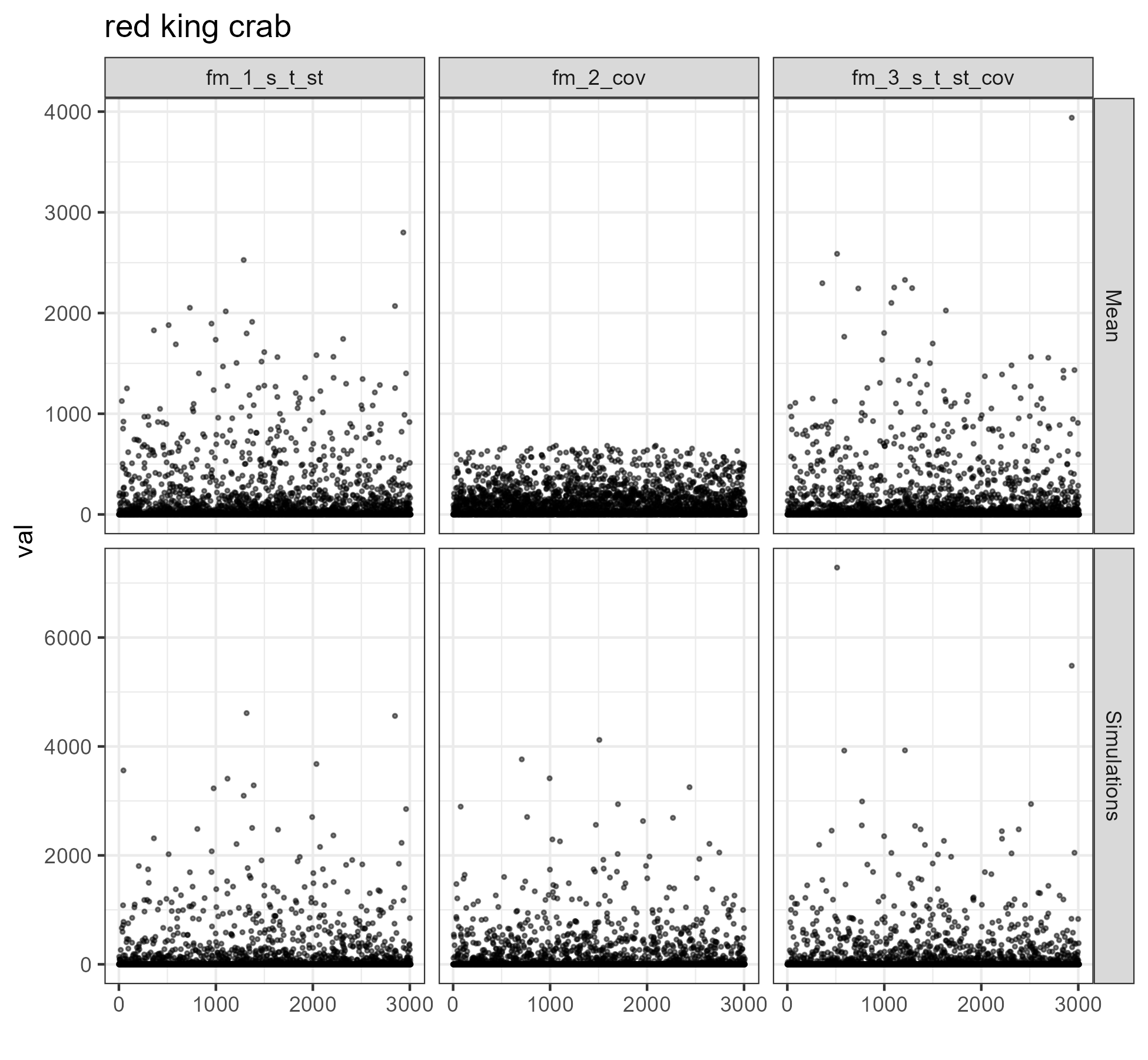
for (i in 1:length(unique(comb$SPECIES))) {
figure <- ggplot2::ggplot(data = dat %>%
dplyr::filter(SPECIES == unique(comb$SPECIES)[i]),
mapping = aes(x = Index, y = val)) +
ggplot2::geom_point(size = .5, alpha = .5) +
ggplot2::facet_grid(rows = vars(type), cols = vars(model), scales = "free_y") +
ggplot2::ggtitle(unique(comb$SPECIES)[i]) +
ggplot2::xlab("")
ggsave(filename = paste0("vigD_model_sim_", unique(comb$SPECIES)[i], ".png"),
path = here::here("vignettes"),
plot = figure,
width = 6.5, height = 6)
}
REPS <- 4
ests <- list()
for(i in 1:nrow(comb)){
cat("Simulating ",comb$SPECIES[i],"\n", comb$fm_name[i], ": ", comb$fm[i], "\n")
temp <- paste0(comb$SPECIES[i], " ", comb$fm_name[i])
# for(SPECIES in specLevels){
ests[[ temp ]] <- list()
## simulate data
csim <- sdmgamindex::get_surveyidx_sim(models[[i]], ds[[comb$SPECIES[i]]])
sims <-lapply(1:REPS,function(j) sdmgamindex::get_surveyidx_sim(
model = models[[i]],
d = ds[[comb$SPECIES[i]]],
sampleFit = FALSE,
condSim = csim) )
## re-estimate
tmp <- ds[[i]]
for(ii in 1:REPS) {
tmp[[2]]$Nage <- matrix(sims[[ii]][[1]][,1],ncol=1)
colnames(tmp$Nage)<-1
ests[[SPECIES]][[ii]] <-
sdmgamindex::get_surveyidx(
x = tmp,
ages = 1,
myids=NULL,
predD=allpd,
cutOff=0,
fam="Tweedie",
modelP=fm,
gamma=1,
control=list(trace=TRUE,maxit=10))
}
}
sims
ests
png(filename = here::here("vignettes","vigD_model_simsest_plot.png"),
width=640*pngscal,
height=480)
# par(mfrow=c(2,2))
save(sims, ests, file = here::here("inst","vigD_model_simsest.Rdata"))
for(i in 1:nrow(comb)){
sdmgamindex::plot_simulation_list(
x = ests[[temp]],
base=models[[temp]],
main=temp,
lwd=2)
}
dev.off()