A more complicated example
To demonstrate more than the basic usage I will use a more complicated model. I modified the ChickWeight random slopes and intercepts example from the RTMB introduction. Modifications include: switching SD parameters to log space and adding a Jacobian, adding broad priors for these SDs, and adding a ‘loglik’ vector for PSIS-LOO (below).
library(RTMB)
parameters <- list(
mua=0, ## Mean slope
logsda=0, ## Std of slopes
mub=0, ## Mean intercept
logsdb=0, ## Std of intercepts
logsdeps=1, ## Residual Std
a=rep(0, 50), ## Random slope by chick
b=rep(0, 50) ## Random intercept by chick
)
f <- function(parms) {
require(RTMB) # for tmbstan
getAll(ChickWeight, parms, warn=FALSE)
sda <- exp(logsda)
sdb <- exp(logsdb)
sdeps <- exp(logsdeps)
## Optional (enables extra RTMB features)
weight <- OBS(weight)
predWeight <- a[Chick] * Time + b[Chick]
loglik <- dnorm(weight, predWeight, sd=sdeps, log=TRUE)
# calculate the target density
lp <- sum(loglik)+ # likelihood
# random effect vectors
sum(dnorm(a, mean=mua, sd=sda, log=TRUE)) +
sum(dnorm(b, mean=mub, sd=sdb, log=TRUE)) +
# broad half-normal priors on SD pars
dnorm(sda, 0, 10, log=TRUE) +
dnorm(sdb, 0, 10, log=TRUE) +
dnorm(sdeps, 0, 10, log=TRUE) +
# jacobian adjustments
logsda + logsdb + logsdeps
# reporting
REPORT(loglik) # for PSIS-LOO
ADREPORT(predWeight) # delta method
REPORT(predWeight) # standard report
return(-lp) # negative log-posterior density
}
obj <- MakeADFun(f, parameters, random=c("a", "b"), silent=TRUE)Asymptotic (frequentist) approximatation vs full posterior
Instead of sampling from the posterior with MCMC (SNUTS), I can use asymptotic tools from TMB to get a quick approximation of the parameters, their covariances, but also uncertainties of generated quantities via the generalized delta method. See the TMB documentation for more background. Briefly, the marginal posterior mode is found and a joint precision matrix determined at the conditional mode. is the covariance of the parameters.
First I optimize the model and call TMB’s sdreport
function to get approximate uncertainties via the delta method and the
joint precision matrix
.
# optimize
opt <- with(obj, nlminb(par, fn, gr))
# get generalized delta method results and Q
sdrep <- sdreport(obj, getJointPrecision=TRUE)
# get the generalized delta method estimates of asymptotic
# standard errors
est <-as.list(sdrep, 'Estimate', report=TRUE)$predWeight
se <- as.list(sdrep, 'Std. Error', report=TRUE)$predWeight
Q <- sdrep$jointPrecision
# can get the joint covariance and correlation like this
Sigma <- as.matrix(solve(Q))
cor <- cov2cor(Sigma)
plot_Q(Q=Q)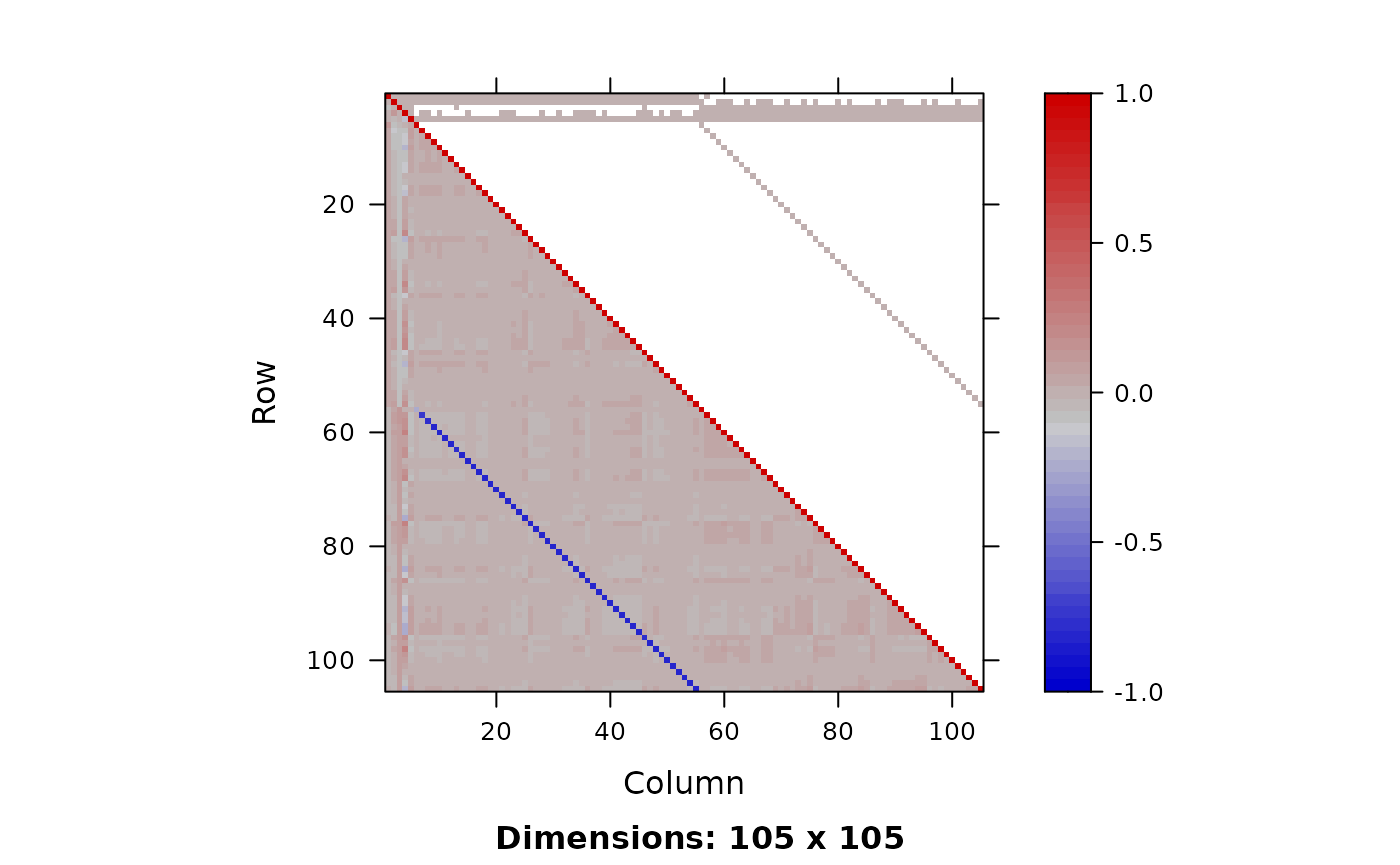
Now I run SNUTS on it and get posterior samples to compare to.
# some very strong negative correlations so I expect a dense or
# sparse metric to be selected with SNUTS. Because I optimized
# above can skip that
mcmc <- sample_snuts(obj, chains=1, init='random', seed=1234,
refresh=0, skip_optimization=TRUE,
Q=Q, Qinv=Sigma)
#> Q is 92.58% zeroes, with condition factor=74028 (min=0.014, max=1018.9)
#> Rebuilding RTMB obj without random effects...
#> dense metric selected b/c faster than sparse and high correlation (max=0.81)
#> log-posterior at inits=(-2627.04); at conditional mode=-2574.481
#> Starting MCMC sampling...
#>
#>
#> Gradient evaluation took 0.000216 seconds
#> 1000 transitions using 10 leapfrog steps per transition would take 2.16 seconds.
#> Adjust your expectations accordingly!
#>
#>
#>
#> Elapsed Time: 0.369 seconds (Warm-up)
#> 1.679 seconds (Sampling)
#> 2.048 seconds (Total)
#>
#>
#>
#> Model 'RTMB' has 105 pars, and was fit using NUTS with a 'dense' metric
#> 1 chain(s) of 1150 total iterations (150 warmup) were used
#> Average run time per chain was 2.05 seconds
#> Minimum ESS=271.1 (27.11%), and maximum Rhat=1.019
#> There were 0 divergences after warmup
post <- as.data.frame(mcmc)
plot_uncertainties(mcmc)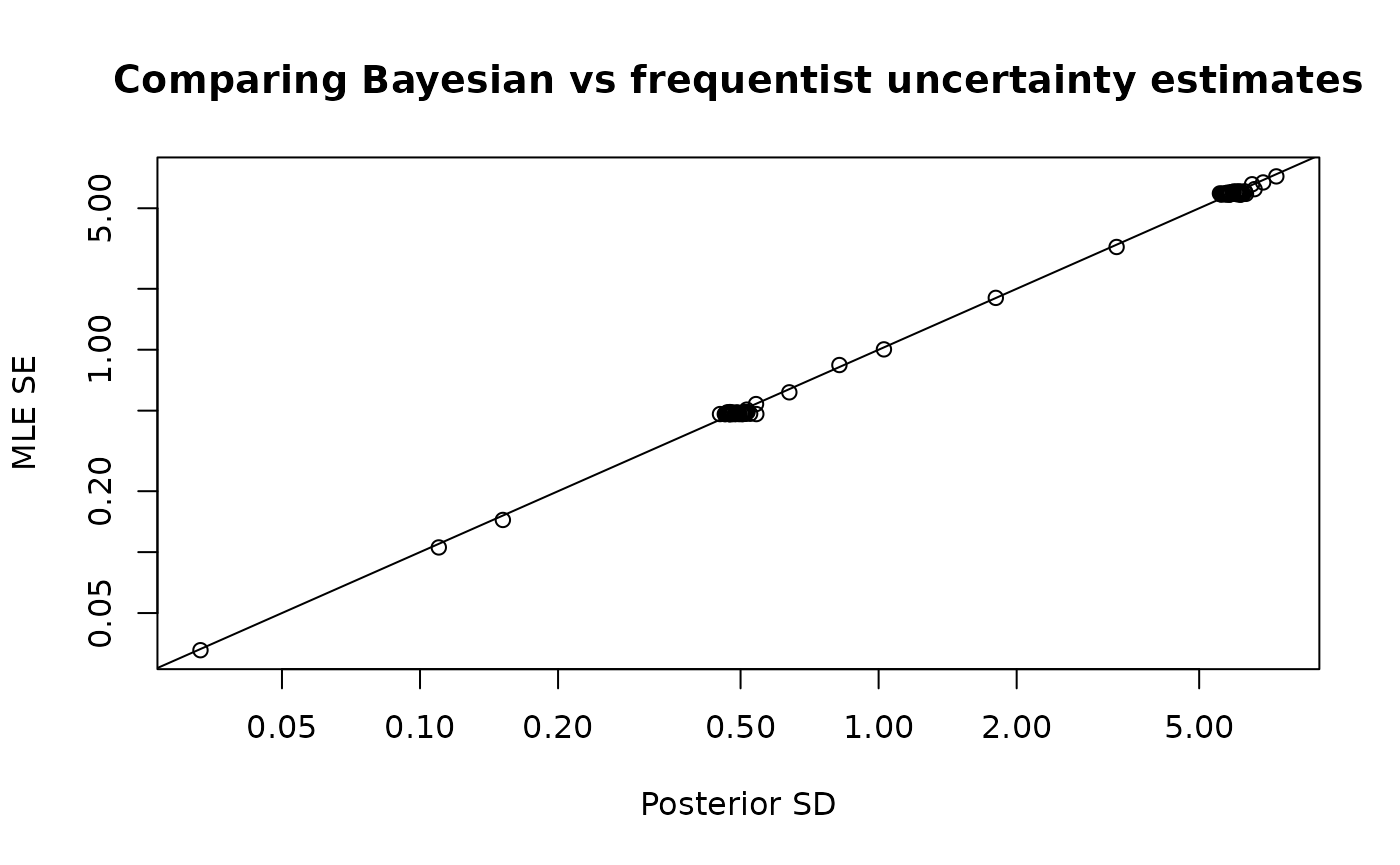
## get posterior of generated quantities
predWeight <- apply(post,1, \(x) obj$report(x)$predWeight) |>
t()
predWeight |> str()
#> num [1:1000, 1:578] 28.1 29.3 23.5 24.8 26.7 ...
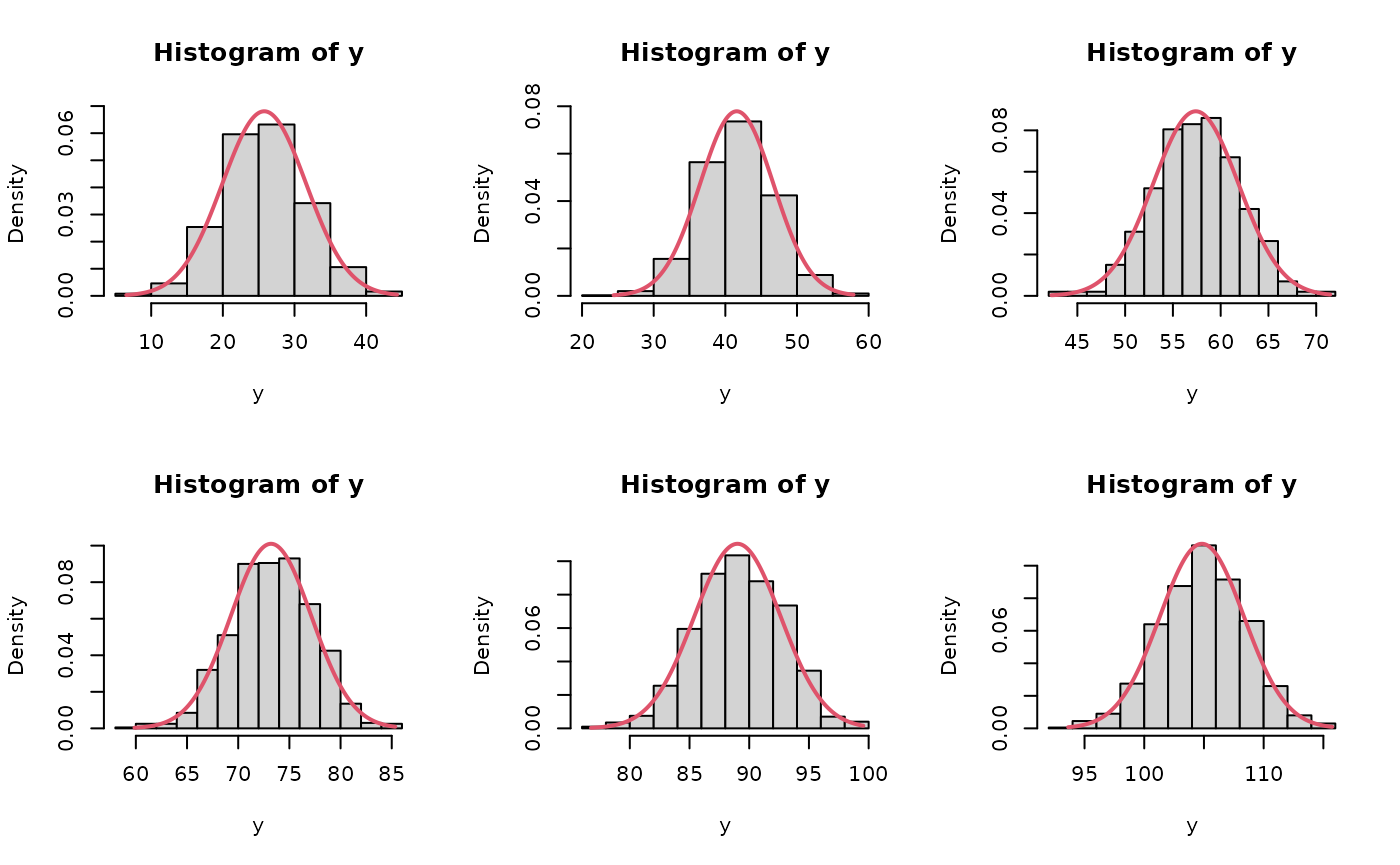
# compare asymptotic vs posterior intervals of first few chicks
par(mfrow=c(2,3))
for(ii in 1:6){
y <- predWeight[,ii]
x <- seq(min(y), max(y), len=200)
y2 <- dnorm(x,est[ii], se[ii])
hist(y, freq=FALSE, ylim=c(0,max(y2)))
lines(x, y2, col=2, lwd=2)
}
dev.off()
#> null device
#> 1Simulation of parameters and data
Simulation of data can be done directly in R. Specialized simulation functionality exists for TMB, and to a lesser degree RTMB, but I keep it simple here for demonstration purposes.
Both data and parameters can be simulated and I explore that below.
Prior and posterior predictive distributions
# simulation of data sets can be done manually in R. For instance
# to get posterior predictive I loop through each posterior
# sample and draw new data.
set.seed(351231)
simdat <- apply(post,1, \(x){
yhat <- obj$report(x)$predWeight
ysim <- rnorm(n=length(yhat), yhat, sd=exp(x['logsdeps']))
}) |> t()
boxplot(simdat[,1:24], main='Posterior predictive')
points(ChickWeight$weight[1:24], col=2, cex=2, pch=16)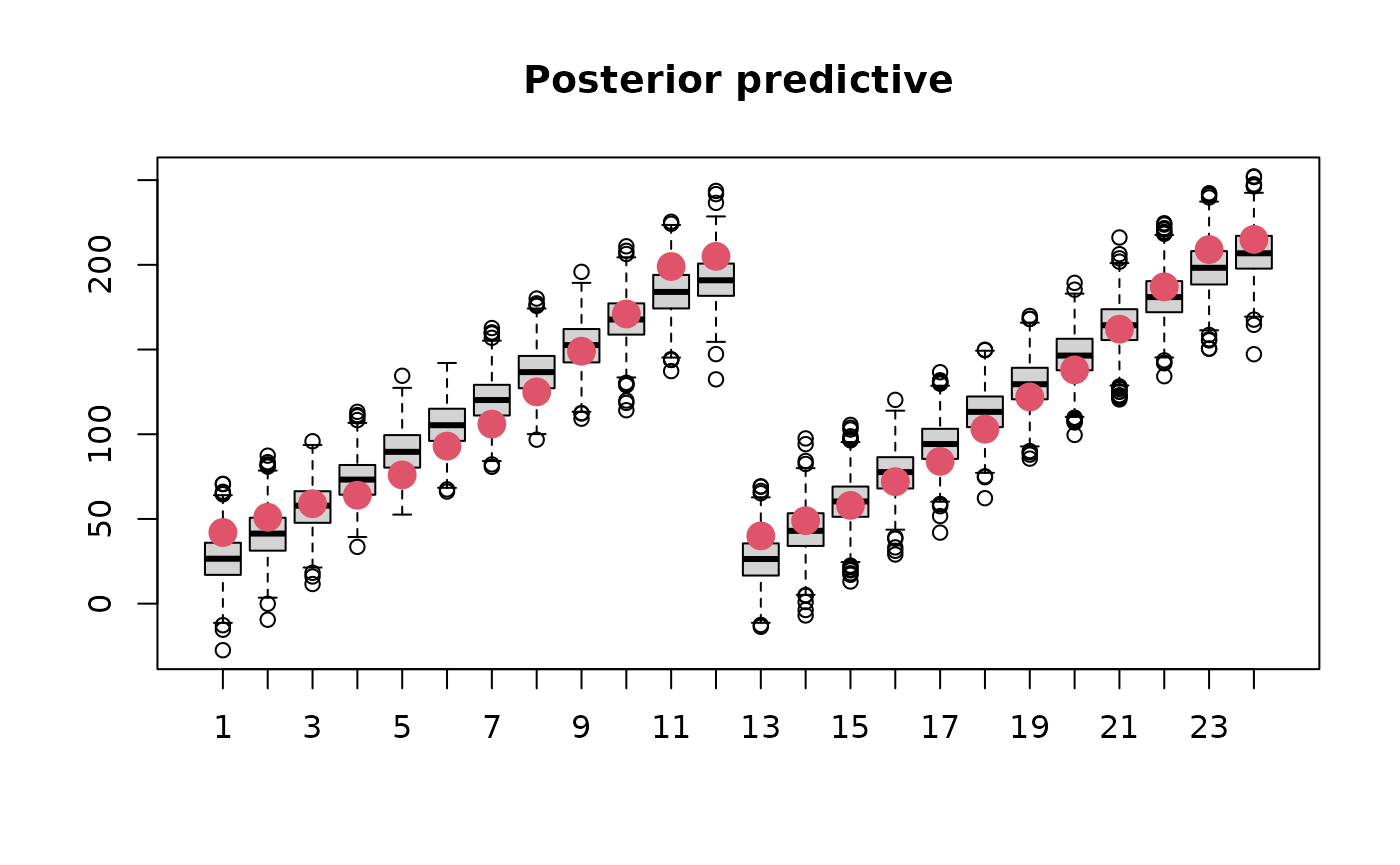
Prior predictive sampling would be done in the same way but is not shown here.
Joint precision sampling
Samples can be drawn from , assuming multivariate normality, as follows:
# likewise I can simulate draws from Q to get approximate samples
postQ <- mvtnorm::rmvnorm(1000, mean=mcmc$mle$est, sigma=Sigma)These samples could be put back into the report function
to get a distribution of a generated quantity, for instance.
Model selection with PSIS-LOO
PSIS-LOO is the recommended way to compare predictive performance of
Bayesian models. I use it to compare a simplified Chicks model below
using the map argument to turn off estimation of the random
intercepts (‘b’). All this requires is for the vector of log-likelihood
values to be available for each posterior draw. I facilitate this via a
REPORT(loglik) call above.
library(loo)
#> This is loo version 2.9.0
#> - Online documentation and vignettes at mc-stan.org/loo
#> - As of v2.0.0 loo defaults to 1 core but we recommend using as many as possible. Use the 'cores' argument or set options(mc.cores = NUM_CORES) for an entire session.
options(mc.cores=parallel::detectCores())
loglik <- apply(post,1, \(x) obj$report(x)$loglik) |>
t()
loo1 <- loo(loglik, cores=4)
#> Warning: Some Pareto k diagnostic values are too high. See help('pareto-k-diagnostic') for details.
print(loo1)
#>
#> Computed from 1000 by 578 log-likelihood matrix.
#>
#> Estimate SE
#> elpd_loo -2351.8 19.9
#> p_loo 88.5 6.9
#> looic 4703.6 39.7
#> ------
#> MCSE of elpd_loo is NA.
#> MCSE and ESS estimates assume independent draws (r_eff=1).
#>
#> Pareto k diagnostic values:
#> Count Pct. Min. ESS
#> (-Inf, 0.67] (good) 572 99.0% 103
#> (0.67, 1] (bad) 6 1.0% <NA>
#> (1, Inf) (very bad) 0 0.0% <NA>
#> See help('pareto-k-diagnostic') for details.
plot(loo1)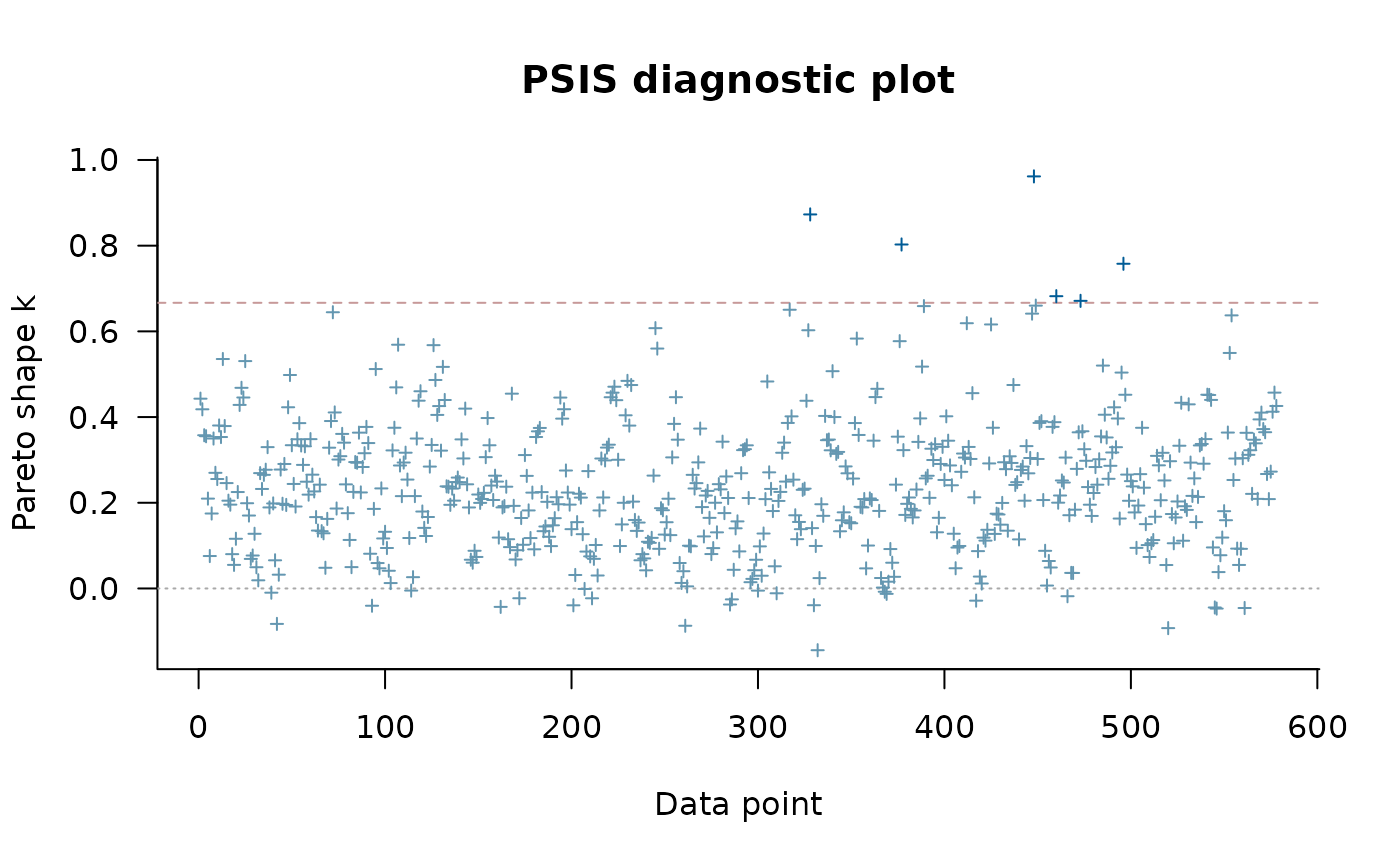
# I can compare that to a simpler model which doesn't have
# random effects on the slope
obj2 <- MakeADFun(f, parameters, random=c("a"), silent=TRUE,
map=list(b=factor(rep(NA, length(parameters$b))),
logsdb=factor(NA),
mub=factor(NA)))
mcmc2 <- sample_snuts(obj2, chains=1, seed=1215, refresh=0)
#> Optimizing...
#> Getting Q...
#> Inverting Q...
#> Q is 88.9% zeroes, with condition factor=8423 (min=0.128, max=1080.5)
#> Rebuilding RTMB obj without random effects...
#> diag metric selected b/c of low correlations (max=0.1386)
#> log-posterior at inits=(-2745.52); at conditional mode=-2745.519
#> Starting MCMC sampling...
#>
#>
#> Gradient evaluation took 0.000139 seconds
#> 1000 transitions using 10 leapfrog steps per transition would take 1.39 seconds.
#> Adjust your expectations accordingly!
#>
#>
#>
#> Elapsed Time: 0.177 seconds (Warm-up)
#> 0.932 seconds (Sampling)
#> 1.109 seconds (Total)
#> Warning: The ESS has been capped to avoid unstable estimates.
#> Warning: The ESS has been capped to avoid unstable estimates.
#>
#>
#> Model 'RTMB' has 53 pars, and was fit using NUTS with a 'diag' metric
#> 1 chain(s) of 1150 total iterations (150 warmup) were used
#> Average run time per chain was 1.11 seconds
#> Minimum ESS=367.1 (36.71%), and maximum Rhat=1.01
#> There were 0 divergences after warmup
post2 <- as.data.frame(mcmc2)
loglik2 <- apply(post2,1, \(x) obj2$report(x)$loglik) |>
t()
loo2 <- loo(loglik2, cores=4)
#> Warning: Some Pareto k diagnostic values are too high. See help('pareto-k-diagnostic') for details.
print(loo2)
#>
#> Computed from 1000 by 578 log-likelihood matrix.
#>
#> Estimate SE
#> elpd_loo -2613.1 14.4
#> p_loo 31.8 3.0
#> looic 5226.2 28.9
#> ------
#> MCSE of elpd_loo is NA.
#> MCSE and ESS estimates assume independent draws (r_eff=1).
#>
#> Pareto k diagnostic values:
#> Count Pct. Min. ESS
#> (-Inf, 0.67] (good) 577 99.8% 195
#> (0.67, 1] (bad) 1 0.2% <NA>
#> (1, Inf) (very bad) 0 0.0% <NA>
#> See help('pareto-k-diagnostic') for details.
loo_compare(loo1, loo2)
#> elpd_diff se_diff
#> model1 0.0 0.0
#> model2 -261.3 19.3Advanced features
Adaptation of Stan diagonal mass matrix
When the estimate of
does not well approximate the posterior surface, then it may be
advantageous to adapt a diagonal mass matrix to account for changes in
scale. This can be controlled via the adapt_stan_metric
argument. This argument is automatically set to FALSE when using a
metric other than ‘stan’ and ‘unit’ since all other metrics in theory
already descale the posterior. This can be overridden by setting it
equal to TRUE
Here I run three versions of the model and compare the NUTS stepsize. The model version without adaptation uses a shorter warmup period
library(ggplot2)
adapted1 <- sample_snuts(obj, chains=1, seed=1234, refresh=0,
skip_optimization=TRUE, Q=Q, Qinv=Sigma,
metric='auto', adapt_stan_metric = TRUE)
#> Q is 92.58% zeroes, with condition factor=74028 (min=0.014, max=1018.9)
#> Rebuilding RTMB obj without random effects...
#> dense metric selected b/c faster than sparse and high correlation (max=0.81)
#> log-posterior at inits=(-2574.48); at conditional mode=-2574.481
#> Starting MCMC sampling...
#>
#>
#> Gradient evaluation took 0.000207 seconds
#> 1000 transitions using 10 leapfrog steps per transition would take 2.07 seconds.
#> Adjust your expectations accordingly!
#>
#>
#>
#> Elapsed Time: 2.502 seconds (Warm-up)
#> 2.425 seconds (Sampling)
#> 4.927 seconds (Total)
#>
#>
#>
#> Model 'RTMB' has 105 pars, and was fit using NUTS with a 'dense' metric
#> 1 chain(s) of 2000 total iterations (1000 warmup) were used
#> Average run time per chain was 4.93 seconds
#> Minimum ESS=282.3 (28.23%), and maximum Rhat=1.016
#> There were 0 divergences after warmup
adapted2 <- sample_snuts(obj, chains=1, seed=1234, refresh=0,
skip_optimization=TRUE, Q=Q, Qinv=Sigma,
metric='stan', adapt_stan_metric = TRUE)
#> Rebuilding RTMB obj without random effects...
#> log-posterior at inits=(-2574.4)
#> Starting MCMC sampling...
#>
#>
#> Gradient evaluation took 0.000123 seconds
#> 1000 transitions using 10 leapfrog steps per transition would take 1.23 seconds.
#> Adjust your expectations accordingly!
#>
#>
#>
#> Elapsed Time: 11.895 seconds (Warm-up)
#> 4.223 seconds (Sampling)
#> 16.118 seconds (Total)
#> Warning: The ESS has been capped to avoid unstable estimates.
#> Warning: The ESS has been capped to avoid unstable estimates.
#> Warning: The ESS has been capped to avoid unstable estimates.
#> Warning: The ESS has been capped to avoid unstable estimates.
#>
#>
#> Model 'RTMB' has 105 pars, and was fit using NUTS with a 'stan' metric
#> 1 chain(s) of 2000 total iterations (1000 warmup) were used
#> Average run time per chain was 16.12 seconds
#> Minimum ESS=345.8 (34.58%), and maximum Rhat=1.016
#> There were 0 divergences after warmup
sp1 <- extract_sampler_params(mcmc, inc_warmup = TRUE) |>
subset(iteration <= 1050) |>
cbind(type='descaled + not adapted')
sp2 <- extract_sampler_params(adapted1, inc_warmup = TRUE) |>
subset(iteration <= 1050) |>
cbind(type='descaled + adapted')
sp3 <- extract_sampler_params(adapted2, inc_warmup = TRUE) |>
subset(iteration <= 1050) |>
cbind(type='adapted')
sp <- rbind(sp1, sp2, sp3)
ggplot(sp, aes(x=iteration, y=stepsize__, color=type)) + geom_line() +
scale_y_log10() + theme_bw() + theme(legend.position = 'top') +
labs(color=NULL, x='warmup')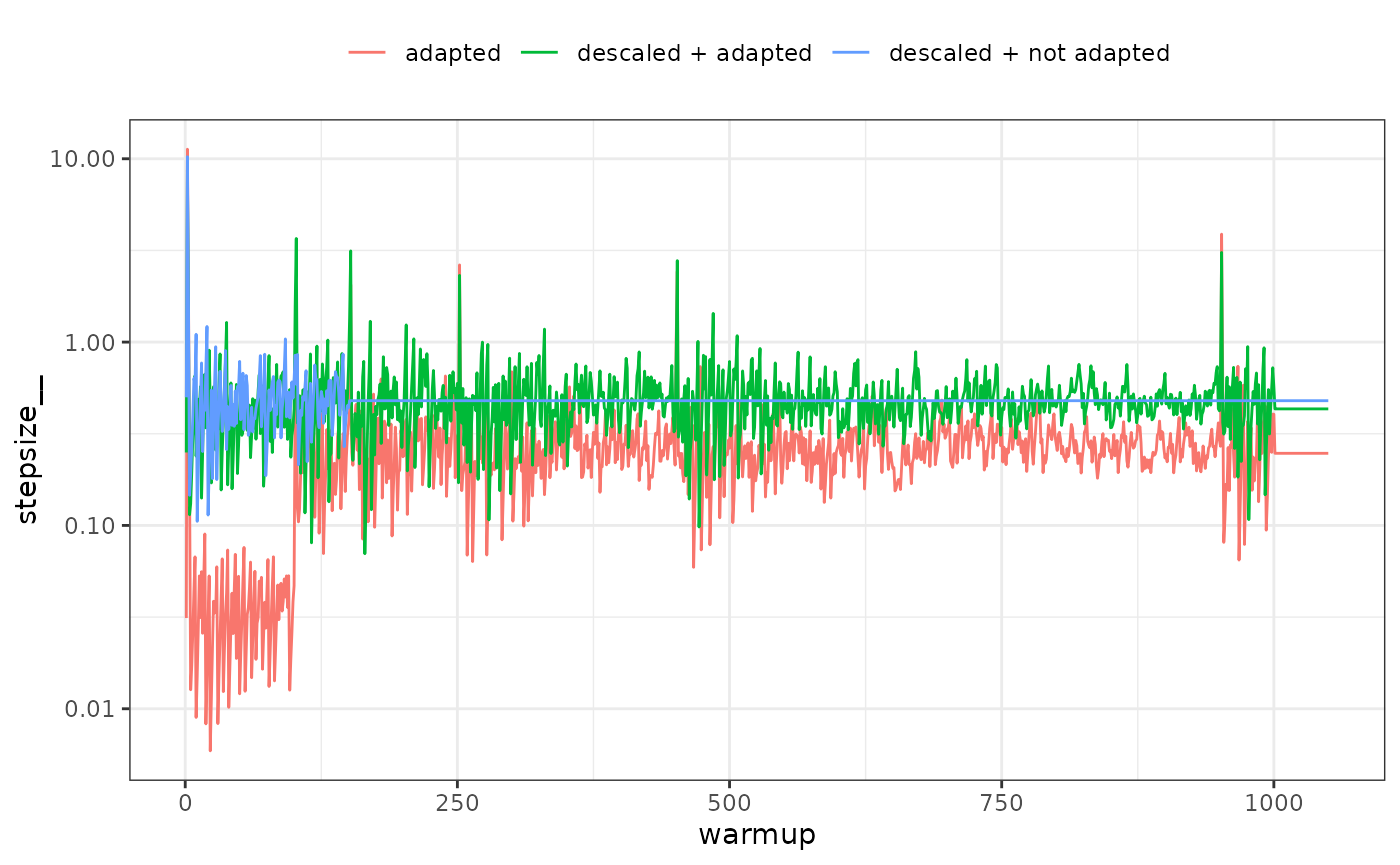
It is apparent that during the first warmup phase the model with Stan defaults (‘adapted’ in the above plot) has a large adjustment in stepsize and this corresponds to very long trajectory lengths and thus increased computational time. If descaled using the adaptation does nothing (‘descaled + adapted’), which is why such a short warmup period can be used with SNUTS (‘descaled + not adapted’) in this case, and often which is why the default warmup is short and adaptation disabled for SNUTS.
In other cases a longer warmup and mass matrix adaptation will make a difference, see for example the ‘wildf’ model in C. C. Monnahan et al. (in prep).
Embedded Laplace approximation SNUTS
This approach uses NUTS (or SNUTS) to sample from the marginal posterior using the Laplace approximation to integrate the random effects. This was first explored in (C. C. Monnahan and Kristensen 2018) and later in more detail in (Margossian et al. 2020) who called it the ‘embedded Laplace approximation’. (C. C. Monnahan et al. in prep) applied this to a much larger set of models and found mixed results.
It is trivial to try in SNUTS by simply declaring
laplace=TRUE.
ela <- sample_snuts(obj, chains=1, laplace=TRUE, refresh=0)
#> Optimizing...
#> Getting M for fixed effects...
#> Qinv is 0% zeroes, with condition factor=3107 (min=0.001, max=3.3)
#> diag metric selected b/c low correlations (max=0.1458)
#> log-posterior at inits=(-2451.94); at conditional mode=-2451.942
#> Starting MCMC sampling...
#>
#>
#> Gradient evaluation took 0.000843 seconds
#> 1000 transitions using 10 leapfrog steps per transition would take 8.43 seconds.
#> Adjust your expectations accordingly!
#>
#>
#>
#> Elapsed Time: 1.193 seconds (Warm-up)
#> 6.905 seconds (Sampling)
#> 8.098 seconds (Total)
#>
#>
#>
#> Model 'RTMB' has 5 pars, and was fit using NUTS with a 'diag' metric
#> 1 chain(s) of 1150 total iterations (150 warmup) were used
#> Average run time per chain was 8.1 seconds
#> Minimum ESS=521.1 (52.11%), and maximum Rhat=1.009
#> There were 0 divergences after warmupHere I can see there are only 5 model parameters (the fixed effects), and that a diagonal metric was chosen due to minimal correlations among these parameters. ELA will typically take longer to run, but have higher minESS and so it is best to compare the efficiency (minESS per time) which I do not do here.
Exploring ELA is a good opportunity to show how SNUTS can fail. I demonstrate this with the notoriously difficult ‘funnel’ model which is a hierarchical model without any data. This model has strongly varying curvature and thus is not well-approximated by so SNUTS mixes poorly. But after turning on ELA, it mixes fine and recovers the
# Funnel example ported to RTMB from
# https://mc-stan.org/docs/cmdstan-guide/diagnose_utility.html#running-the-diagnose-command
## the (negative) posterior density as a function in R
f <- function(pars){
getAll(pars)
lp <- dnorm(y, 0, 3, log=TRUE) + # prior
sum(dnorm(x, 0, exp(y/2), log=TRUE)) # likelihood
return(-lp) # TMB expects negative log posterior
}
obj <- RTMB::MakeADFun(f, list(y=-1.12, x=rep(0,9)), random='x', silent=TRUE)
### Now SNUTS
fit <- sample_snuts(obj, seed=1213, refresh=0, init='random')
#> Optimizing...
#> Getting Q...
#> Inverting Q...
#> Q is 100% zeroes, with condition factor=9 (min=0.111, max=1)
#> Rebuilding RTMB obj without random effects...
#> diag metric selected b/c of low correlations (max=0)
#> log-posterior at inits=(-237.12,-23.12,-37.52,-20.55); at conditional mode=-10.288
#> Starting MCMC sampling...
#> Preparing parallel workspace...
#> Chain 1: Gradient evaluation took 0.000171 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 1.71 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 2: Gradient evaluation took 0.000234 seconds
#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 2.34 seconds.
#> Chain 2: Adjust your expectations accordingly!
#> Chain 3: Gradient evaluation took 0.000216 seconds
#> Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 2.16 seconds.
#> Chain 3: Adjust your expectations accordingly!
#> Chain 4: Gradient evaluation took 0.000202 seconds
#> Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 2.02 seconds.
#> Chain 4: Adjust your expectations accordingly!
#> Chain 4: Elapsed Time: 1.456 seconds (Warm-up)
#> Chain 4: 6.883 seconds (Sampling)
#> Chain 4: 8.339 seconds (Total)
#> Chain 2: Elapsed Time: 4.496 seconds (Warm-up)
#> Chain 2: 11.366 seconds (Sampling)
#> Chain 2: 15.862 seconds (Total)
#> Chain 1: Elapsed Time: 1.765 seconds (Warm-up)
#> Chain 1: 15.879 seconds (Sampling)
#> Chain 1: 17.644 seconds (Total)
#> Chain 3: Elapsed Time: 1.221 seconds (Warm-up)
#> Chain 3: 21.769 seconds (Sampling)
#> Chain 3: 22.99 seconds (Total)
#>
#>
#> Model 'RTMB' has 10 pars, and was fit using NUTS with a 'diag' metric
#> 4 chain(s) of 1150 total iterations (150 warmup) were used
#> Average run time per chain was 16.21 seconds
#> Minimum ESS=44.4 (1.11%), and maximum Rhat=1.081
#> !! Warning: Signs of non-convergence found. Do not use for inference !!
#> There were 9 divergences after warmup
pairs(fit, pars=1:2)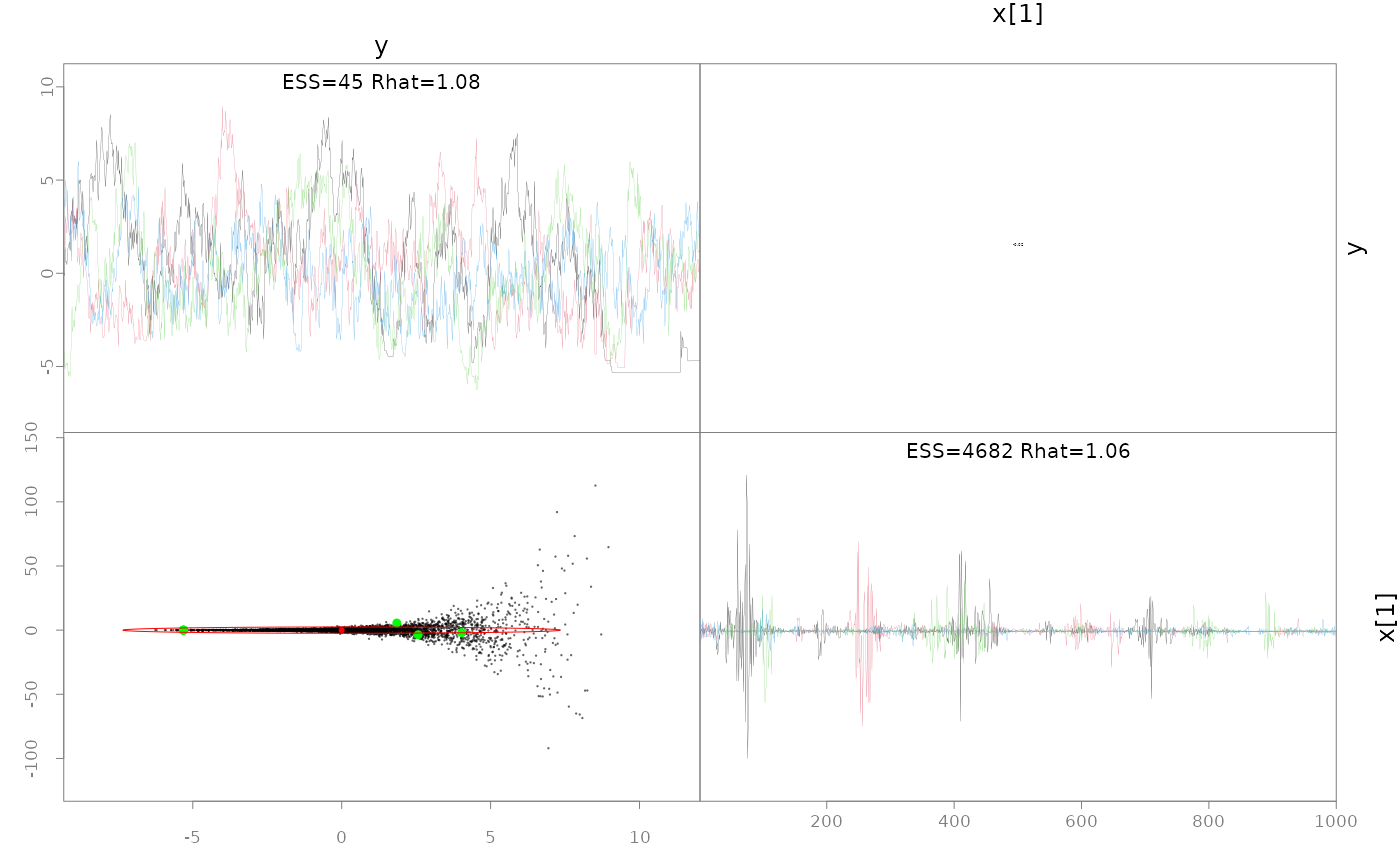
# hasn't recovered the prior b/c it's not converged, particularly
# for small y values
post <- as.data.frame(fit)
hist(post$y, freq=FALSE, xlim=c(-10,10))
lines(x<-seq(-10,10, len=200), dnorm(x,0,3))
abline(v=fit$mle$est[1], col=2, lwd=2)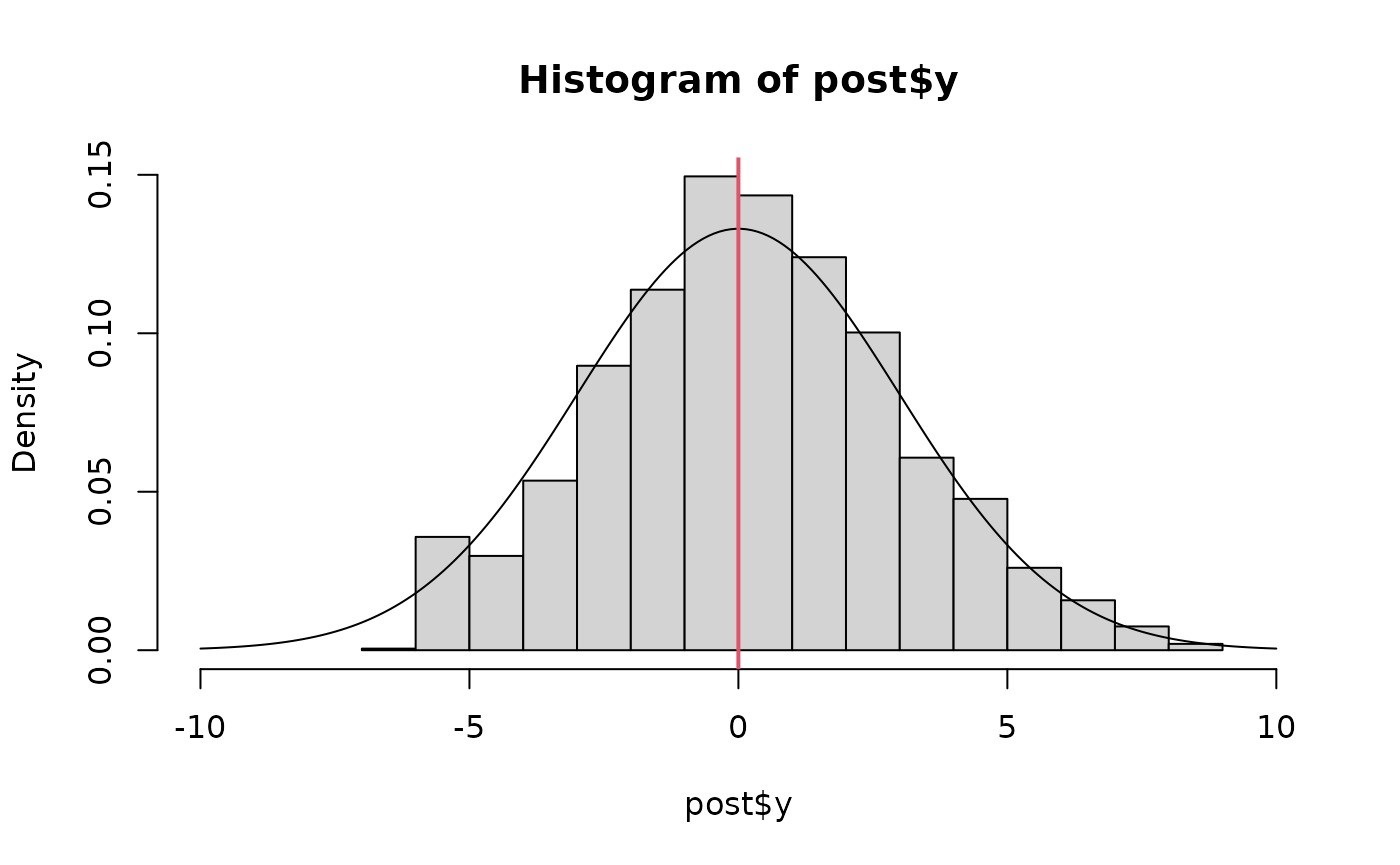
# Now turn on ELA and it easily recovers the prior on y
fit.ela <- sample_snuts(obj, laplace=TRUE, refresh=0, init='random', seed=12312)
#> Optimizing...
#> Getting M for fixed effects...
#> diag metric selected b/c only 1 parameter
#> log-posterior at inits=(-2.68,-2.25,-2.1,-2.08); at conditional mode=-2.018
#> Starting MCMC sampling...
#> Preparing parallel workspace...
#> Chain 1: Gradient evaluation took 0.029226 seconds
#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 292.26 seconds.
#> Chain 1: Adjust your expectations accordingly!
#> Chain 2: Gradient evaluation took 0.047664 seconds
#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 476.64 seconds.
#> Chain 2: Adjust your expectations accordingly!
#> Chain 3: Gradient evaluation took 0.0396 seconds
#> Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 396 seconds.
#> Chain 3: Adjust your expectations accordingly!
#> Chain 4: Gradient evaluation took 0.036212 seconds
#> Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 362.12 seconds.
#> Chain 4: Adjust your expectations accordingly!
#> Chain 2: Elapsed Time: 0.612 seconds (Warm-up)
#> Chain 2: 3.224 seconds (Sampling)
#> Chain 2: 3.836 seconds (Total)
#> Chain 1: Elapsed Time: 0.728 seconds (Warm-up)
#> Chain 1: 3.528 seconds (Sampling)
#> Chain 1: 4.256 seconds (Total)
#> Chain 4: Elapsed Time: 0.678 seconds (Warm-up)
#> Chain 4: 3.299 seconds (Sampling)
#> Chain 4: 3.977 seconds (Total)
#> Chain 3: Elapsed Time: 0.75 seconds (Warm-up)
#> Chain 3: 3.41 seconds (Sampling)
#> Chain 3: 4.16 seconds (Total)
#>
#>
#> Model 'RTMB' has 1 pars, and was fit using NUTS with a 'diag' metric
#> 4 chain(s) of 1150 total iterations (150 warmup) were used
#> Average run time per chain was 4.06 seconds
#> Minimum ESS=1705.7 (42.64%), and maximum Rhat=1.001
#> There were 0 divergences after warmup
# you just get the prior back b/c the Laplace approximation is
# accurate
pairs(fit.ela)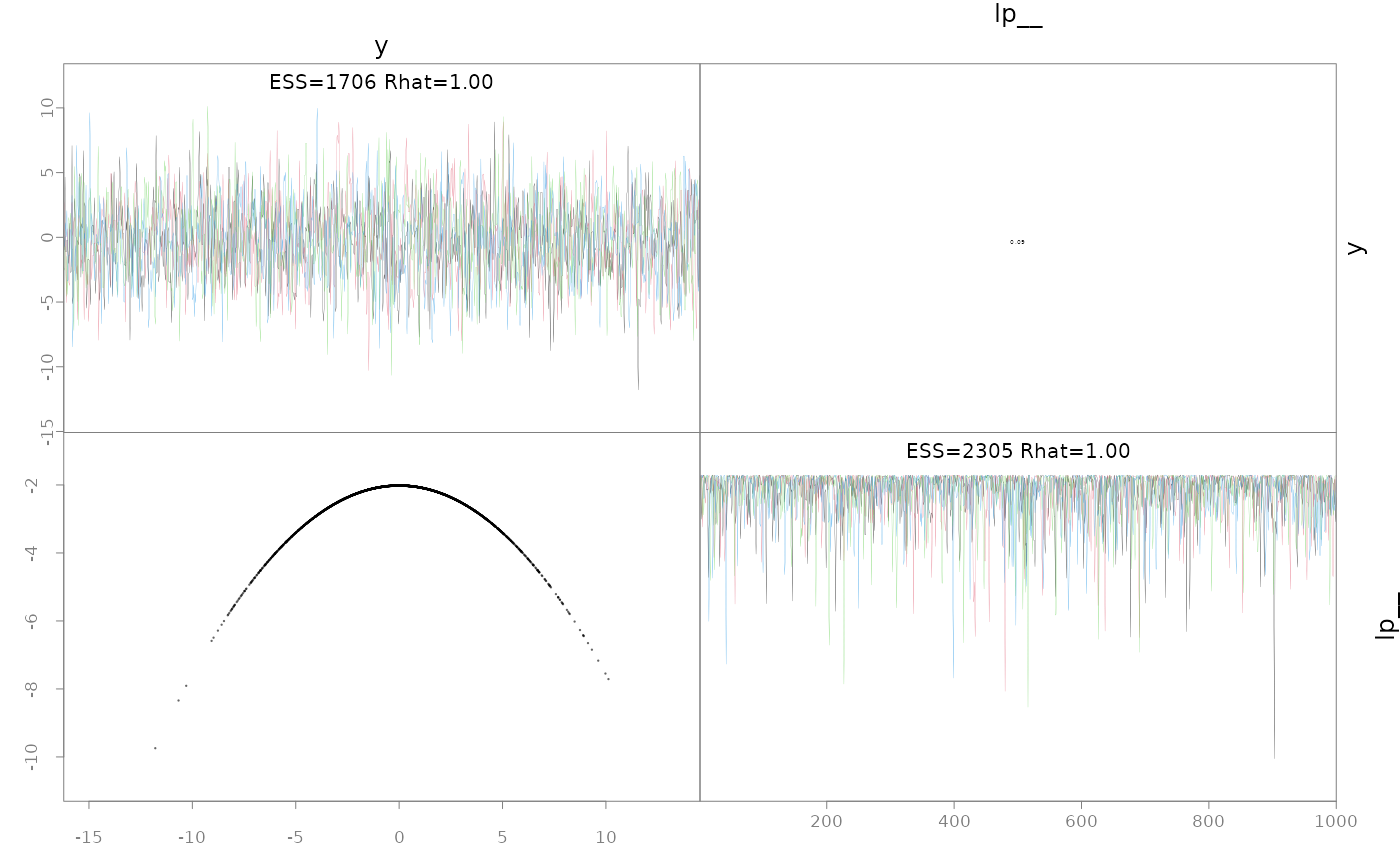
post.ela <- as.data.frame(fit.ela)
hist(post.ela$y, freq=FALSE, breaks=30)
lines(x<-seq(-10,10, len=200), dnorm(x,0,3))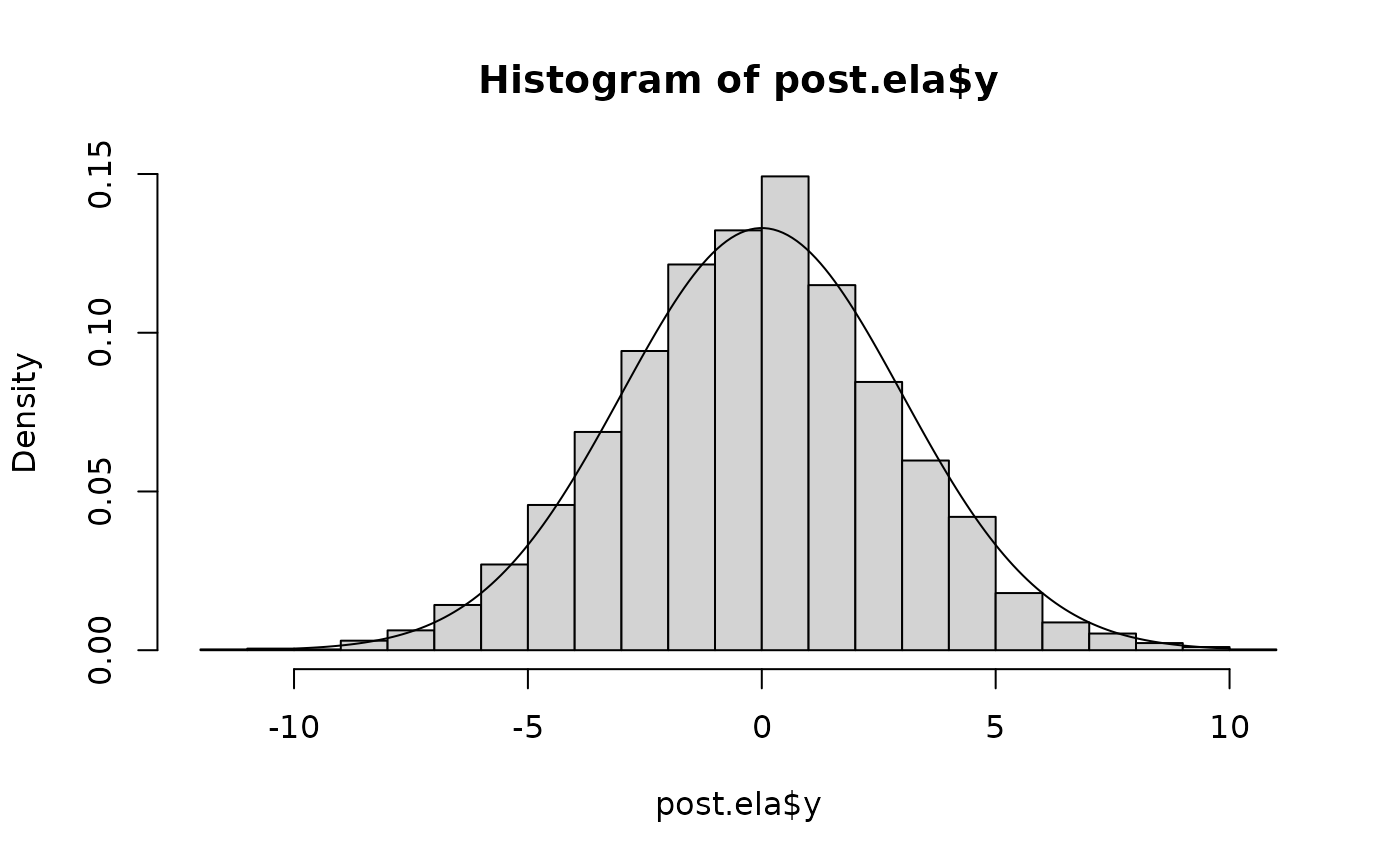
Linking to other Stan algorithms via StanEstimators
sample_snuts links to the
StanEstimators::stan_sample function for NUTS sampling.
However, this package provides other algorithms given a model and these
may be of interest to some users. I focus on the Pathfinder algorithm
and an RTMB model.
# Construct a joint model (no random effects)
obj2 <- MakeADFun(func=obj$env$data, parameters=obj$env$parList(),
map=obj$env$map, random=NULL, silent=TRUE)
# TMB does negative log densities so convert to form used by Stan
fn <- function(x) -obj2$fn(x)
grad_fun <- function(x) -obj2$gr(x)
pf <- StanEstimators::stan_pathfinder(fn=fn, grad_fun=grad_fun, refresh=100,
par_inits = obj$env$last.par.best)
#>
#> Path [1] :Initial log joint density = -10.287998
#> Path [1] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 2 8.084e+01 3.600e+01 4.441e-15 1.000e+00 1.000e+00 62 -4.719e+01 -1.039e+21
#> Path [1] :Best Iter: [1] ELBO (-47.190904) evaluations: (62)
#> Path [2] :Initial log joint density = -10.287998
#> Path [2] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 2 8.084e+01 3.600e+01 4.441e-15 1.000e+00 1.000e+00 62 -3.697e+01 -3.463e+20
#> Path [2] :Best Iter: [1] ELBO (-36.969758) evaluations: (62)
#> Path [3] :Initial log joint density = -10.287998
#> Path [3] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 2 8.084e+01 3.600e+01 4.441e-15 1.000e+00 1.000e+00 62 -4.967e+01 -7.747e+20
#> Path [3] :Best Iter: [1] ELBO (-49.669086) evaluations: (62)
#> Path [4] :Initial log joint density = -10.287998
#> Path [4] : Iter log prob ||dx|| ||grad|| alpha alpha0 # evals ELBO Best ELBO Notes
#> 2 8.084e+01 3.600e+01 4.441e-15 1.000e+00 1.000e+00 62 -4.047e+01 -6.973e+19
#> Path [4] :Best Iter: [1] ELBO (-40.474254) evaluations: (62)
#> Pareto k value (1.3) is greater than 0.7. Importance resampling was not able to improve the approximation, which may indicate that the approximation itself is poor.Linking to other Bayesian tools
It is straightforward to pass SparseNUTS output into
other Bayesian R packages. I demonstrate this with
bayesplot.
library(bayesplot)
#> This is bayesplot version 1.15.0
#> - Online documentation and vignettes at mc-stan.org/bayesplot
#> - bayesplot theme set to bayesplot::theme_default()
#> * Does _not_ affect other ggplot2 plots
#> * See ?bayesplot_theme_set for details on theme setting
library(tidyr)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
post <- as.data.frame(mcmc)
pars <- mcmc$par_names[1:6]
mcmc_areas(post, pars=pars)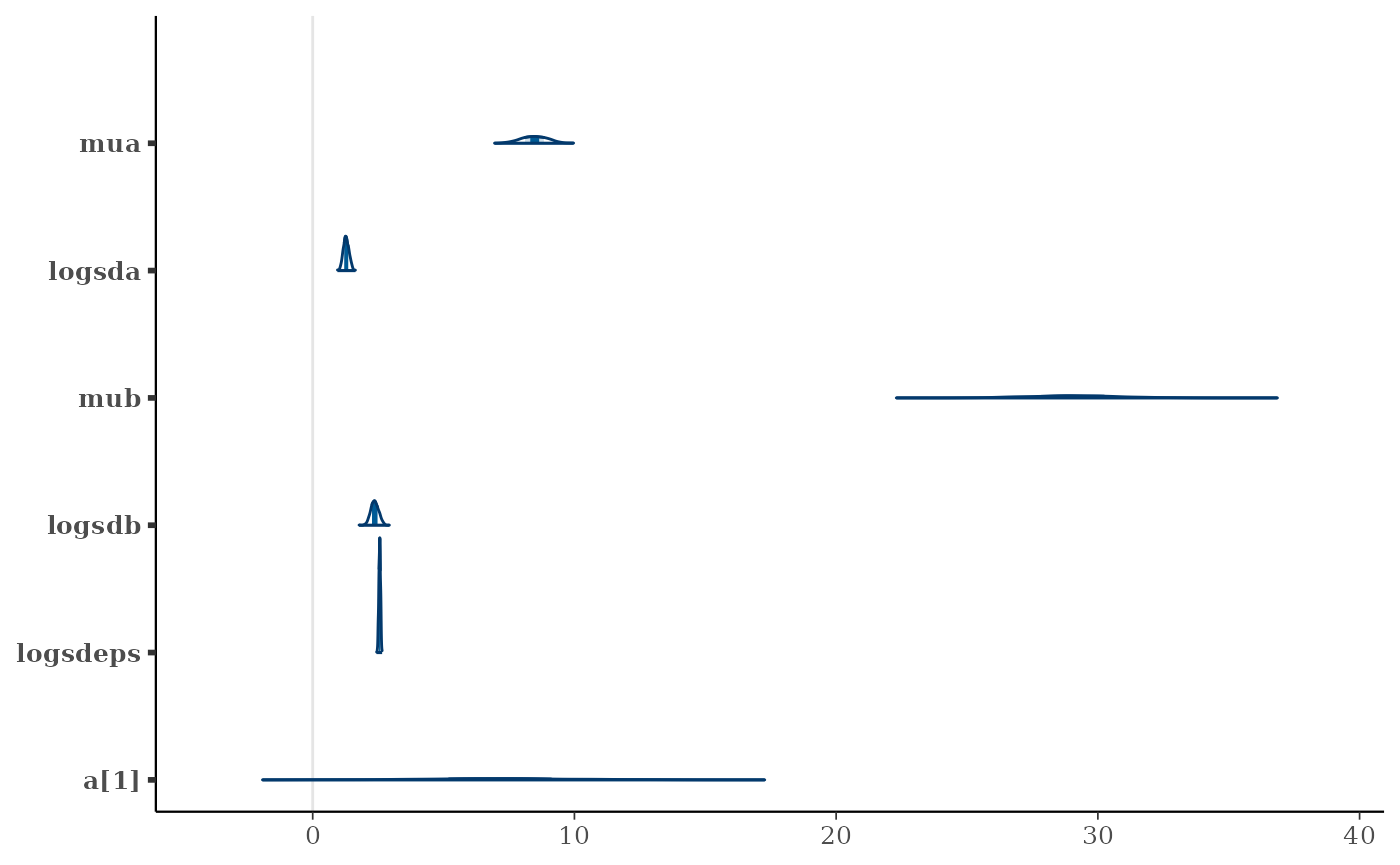
mcmc_trace(post, pars=pars)
color_scheme_set("red")
np <- extract_sampler_params(fit) %>%
pivot_longer(-c(chain, iteration), names_to='Parameter', values_to='Value') %>%
select(Iteration=iteration, Parameter, Value, Chain=chain) %>%
mutate(Parameter=factor(Parameter),
Iteration=as.integer(Iteration),
Chain=as.integer(Chain)) %>% as.data.frame()
mcmc_nuts_energy(np) + ggtitle("NUTS Energy Diagnostic") + theme_minimal()
#> `stat_bin()` using `bins = 30`. Pick better value `binwidth`.
#> `stat_bin()` using `bins = 30`. Pick better value `binwidth`.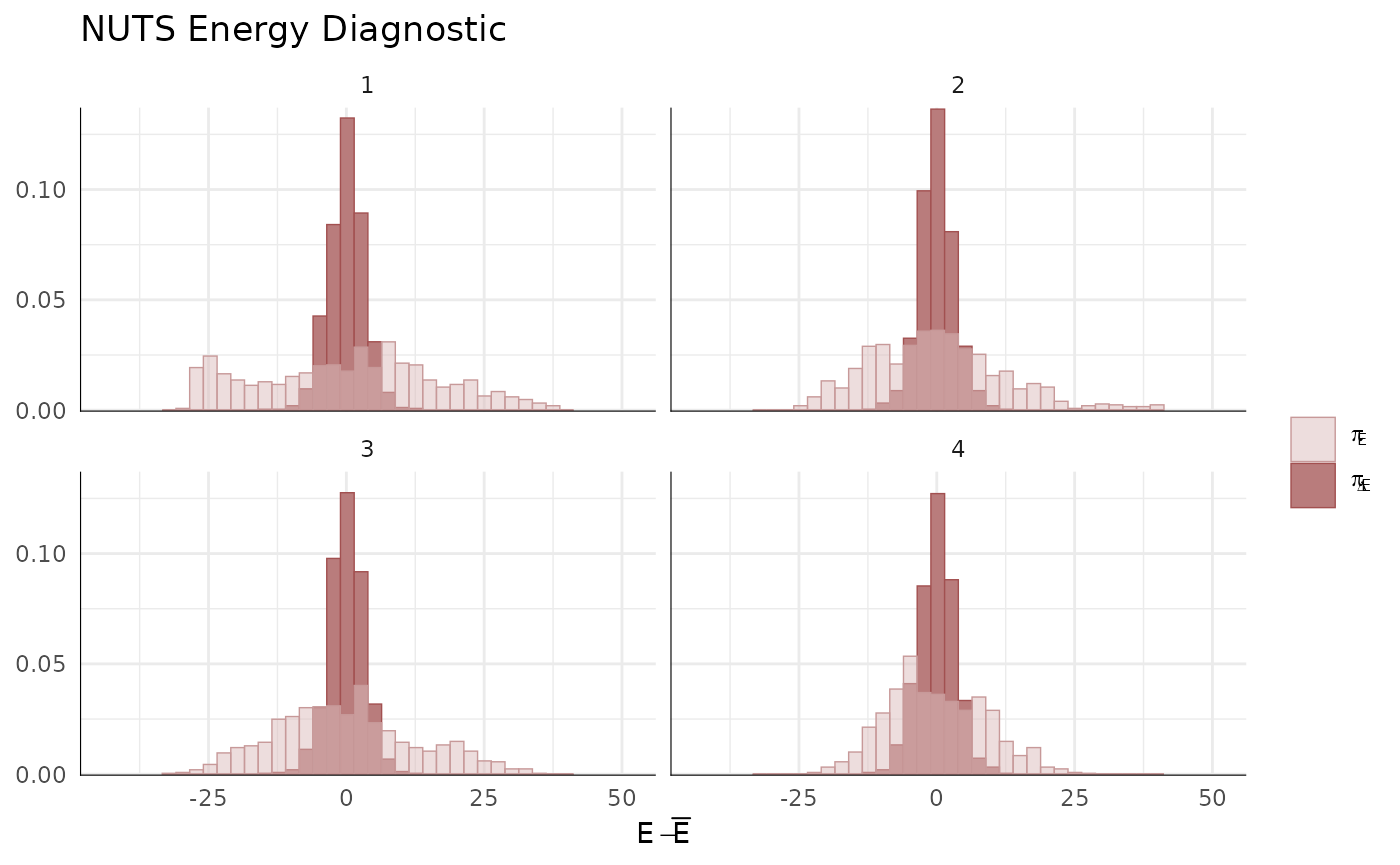
# finally, posterior predictive for first 24 observations
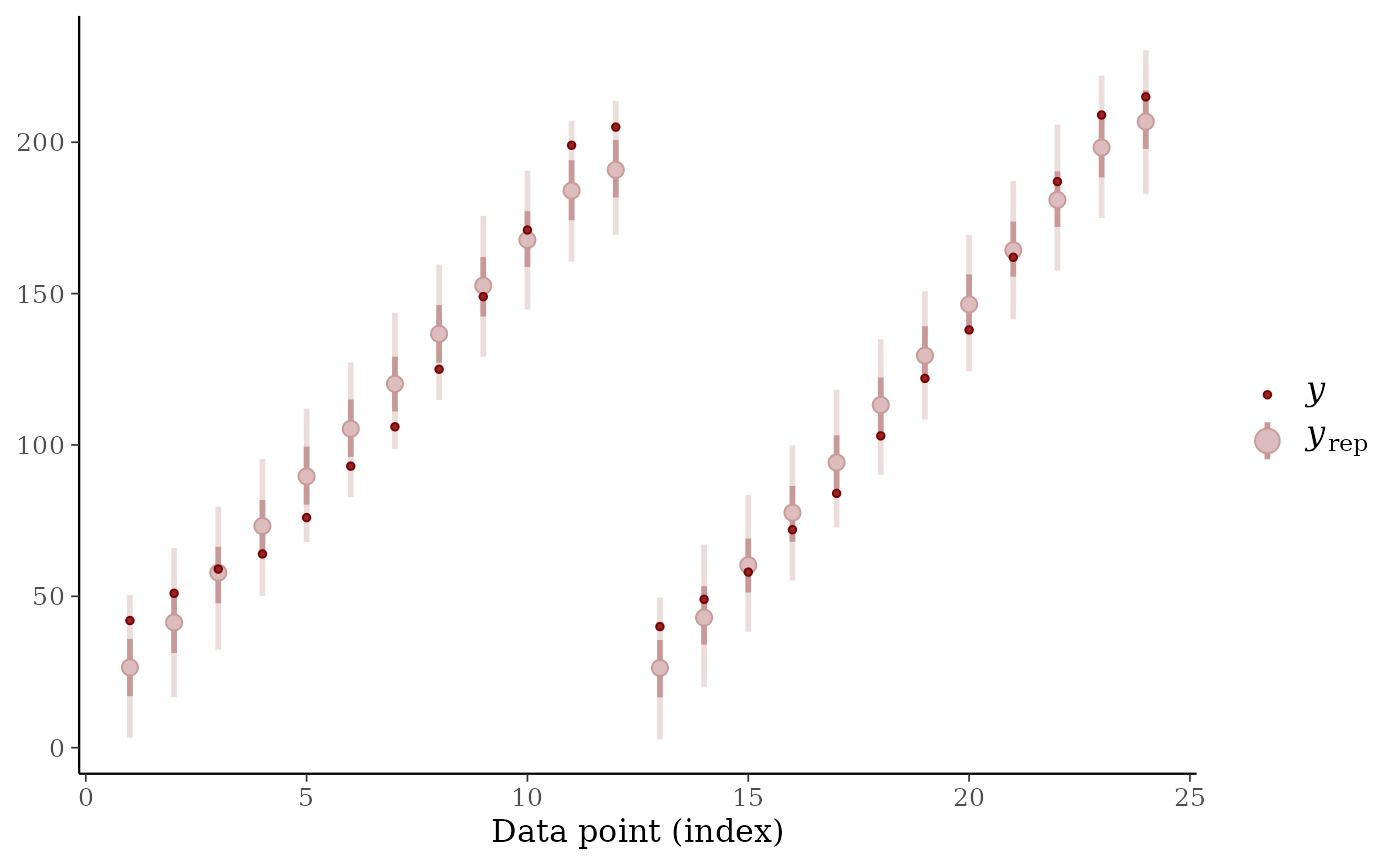
ppc_intervals(y=ChickWeight$weight[1:24], yrep=simdat[,1:24])
#> Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
#> ℹ Please use `linewidth` instead.
#> ℹ The deprecated feature was likely used in the bayesplot package.
#> Please report the issue at <https://github.com/stan-dev/bayesplot/issues/>.
#> This warning is displayed once per session.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.
References
Margossian, Charles, Aki Vehtari, Daniel Simpson, and Raj Agrawal. 2020.
“Hamiltonian Monte Carlo Using an
Adjoint-Differentiated Laplace Approximation:
Bayesian Inference for Latent Gaussian Models
and Beyond.” In Advances in Neural
Information Processing
Systems, edited by H. Larochelle, M. Ranzato, R.
Hadsell, M. F. Balcan, and H. Lin, 33:9086–97. Curran Associates, Inc.
https://proceedings.neurips.cc/paper_files/paper/2020/file/673de96b04fa3adcae1aacda704217ef-Paper.pdf.
Monnahan, C. C, and Kasper Kristensen. 2018. “No-u-Turn Sampling
for Fast Bayesian Inference in ADMB and TMB: Introducing the Adnuts and
Tmbstan r Packages.” PloS One 13 (5).
Monnahan, C. C., Thorson J. T., K. Kristensen, and B. Carpenter. in
prep. “Leveraging Sparsity to Improve No-u-Turn Sampling
Efficiency for Hierarchical Bayesian Models.” arXiv
Preprint, in prep.